Seja a reta que melhor ajusta os dados da tabela abaixo, no sentido dos mínimos quadrados.
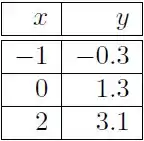
Então o coeficiente vale:
Passo 1
Primeiro vamos escrever essa tabela na forma de um sistema! Como a equação da reta é , basta substituir os pares e que teremos:
Agora passamos isso pra forma matricial:
Passo 2
Mas como o próprio enunciado dá a entender, esse sistema não possui solução! Então vamos aproximá-lo por mínimos quadrados usando a fórmula:
Resposta
Letra