Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio de Stevin

Ver Teoria
Exercício 28123456789101112131415161718192021222324252627293031323334353637

Enunciado

Física 3 - UFF; P1 de 2019.2

14 - Um tubo em forma de U com os extremos abertos, de seção reta uniforme, contém água (densidade de 1   g / c m 3 ) inicialmente a uma altura de 10   c m desde a parte inferior de cada braço. Um líquido imiscível de densidade 2   g / c m 3 é adicionado a um dos braços até que forme uma camada de 4   c m de altura como indicado na figura. Qual é a relação das alturas h 1 / h 2 de líquido nos dois braços?

  1. 2 / 3
  2. 1 / 2
  3. 5 / 7
  4. 2 / 5
  5. 4 / 5

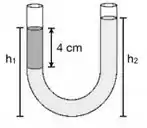
Passo 1

Poxa, vamos separar esses h s aí da seguinte forma:

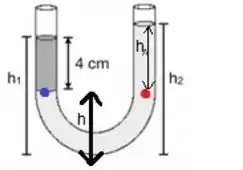
De modo que...

h 1 - h = 4   c m

E...

h 2 - h = h A

Ora, podemos falar que a pressão que o líquido de maior densidade (liquido cinza) faz no ponto azul, é a mesma que a coluna no lado direto faz no ponto vermelho:

ρ c i n z a g ⋅ h 1 - h = ρ g ⋅ h 2 - h   →

4 ⋅ ρ c i n z a = ρ h A   →

Substituindo então as densidades onde ρ c i n z a = 2   g / c m 3 e ρ = 1   g / c m 3 ...

4 ⋅ 2 = h A   →

h A = 8   c m

Passo 2

Beleza! Então com isso temos que...

h 1 - h = 4   c m

E...

h 2 - h = 8   c m

Ainda temos que encontrar mais uma equação para resolver isso aí em h 1 e h 2 !

Sabemos que inicialmente tínhamos uma altura de 10   c m em cada perna (totalizando 20   c m de líquido). Esse 20   c m foram redistribuídos em 2 h (um de um lado e outro de outro) mais h A = 8 (veja aqui na figura):

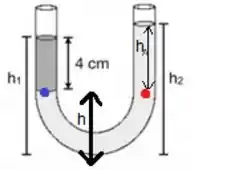
Então...

2 h + 8 = 20

Logo...

2 h = 12   →

h = 6

Então...

h 1 - 6 = 4   c m       →           h 1 = 10   c m

E...

h 2 - 6 = 8   c m               →                 h 2 = 14   c m

Então...

h 1 h 2 = 10 14 =

5 / 7

Resposta

Letra C.

Exercícios de Livros Relacionados

Dois recipientes cilíndricos iguais, com as bases no mesmo nível, contêm um líquido de massa específica 1,30 × 10 ³k g / m ³ . ³ ³ A área de cada base é 4,00c m ² ², mas em um dos recipientes a altura
(Homens e elefantes fazendo snorkel) Quando uma pessoa faz snorkel, os pulmões estão conectados diretamente a atmosfera através do tubo de respiração e, portanto, se encontram a pressão atmosférica. Q
Os cientistas encontraram indícios de que Marte pode ter tido outrora um oceano com 0,500km de profundidade. A aceleração da gravidade em Marte é 3,71 m / s 2 . (a) Qul seria a pressão manométrica no
Um barril contém uma camada de óleo de 0,120m flutuando sobre a água com uma profundidade igual a 0,250m. A densidade do óleo é igual a 600 k g / m 3 . (a) Qual é a pressão manométrica na interface en
A figura mostra um tubo em forma de U modificado: o lado direito é mais curto que o esquerdo. A extremidade do lado direito está d = 10,0c m acima da bancada do laboratório. O raio do tubo é 1,50c m .