O recipiente mostrado na figura abaixo contém um líquido de densidade . Seu lado direito é fechado por um pistão móvel de massa e seção reta . Seu lado esquerdo, de seção reta , não está fechado e um cilindro de massa e volume flutua sobre o líquido. Seja e as alturas do líquido nos lados direito e esquerdo, respectivamente, relativas a um mesmo nível horizontal, como indicado na figura. A constante gravitacional é . A altura é dada por:
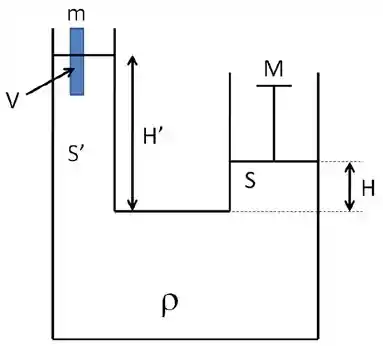
(a)
(b)
(c)
(d)
Passo 1
Vamos primeiro falar do cilindro de massa .
De início, vou te falar uma coisa. Ele não influencia em nada do que queremos calcular!!!COMO ASSIM?!?!!?! É.. meua migo... o IF é brabo!!
Vamos entender o porquê dele não influenciar no que queremos calcular.Imagine a situação onde não tem nem cilindro e nem pistão em nosso recipiente. O que a gente veria seria o seguinte:
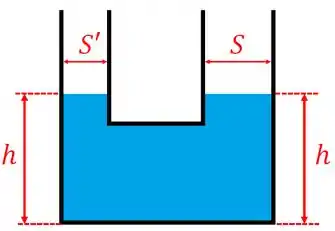
Nessa situação, ambos os lados do nosso recipiente estaria a mesma altura da base. Isso é consequência da Lei de Stevin. Só lembre de não confundir a altura com a altura que o exercício fala!!!
Agora, imagine que seja colocado o cilindro no tubo esquerdo. O que acontece é que os dois tubos (direito e esquerdo) aumentarão seus níveis (a altura ), mas ainda estarão a mesma distância da base (a altura ). Veja a figura.
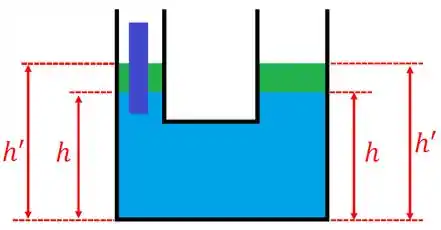
Coloquei em verde o quanto subiu do fluido devido ao cilindro. Novamente, não confunda a altura com a altura que o enunciado fala.
Por que a mesma altura ? Isso acontece porque o cilindro faz o fluido ocupar um volume menor, forçando a subir o nível. Como ambos os lados do recipiente estão expostos ao ar, então na superfície do fluido (tanto lado direito quanto esquerdo) a pressão será igual a pressão atmosférica. Por isso a mesma altura .
Assim, a conclusão que chegamos é que colocar o cilindro só aumenta o nível do fluido!Beleza! Vamos guardar essa informação. Agora imagine que o pistão seja colocado do lado direito do recipiente SEM O CILINDRO do lado esquerdo. O que veremos é
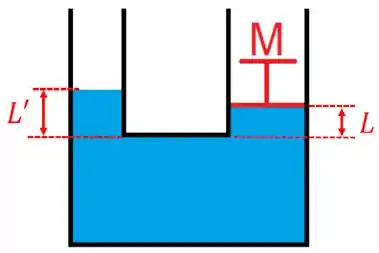
Assim, vai existir uma diferença entre as alturas, pois as pressões serão diferentes entre os lados (o pistão veda o lado direito e a força peso do objeto de massa empurra o pistão para baixo). Vamos chamar de a seguinte diferença
Agora se colocarmos o cilindro do lado direito, sabemos que ele apenas aumentará o nível do fluido igualmente em ambos os lados do recipiente. Assim, o que veremos é
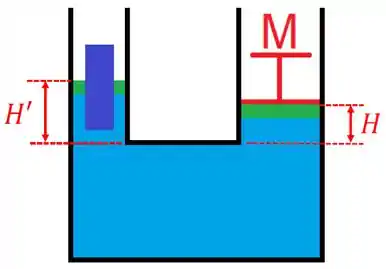
Nesta figura, teremos e agora SÃO as alturas que o enunciado fala. Nesta situação, o cilindro aumenta ambos os lado do recipiente igualmente. Assim, a diferença será igual a diferença , isto é,
Agora podemos traçar nossa estratégia. Primeiro, vamos calcular e . Depois, utilizaremos a equação anterior para determinar . Vamos então para o nosso próximo passo.
Passo 2
Vamos calcular . Para tanto, considere a figura abaixo.
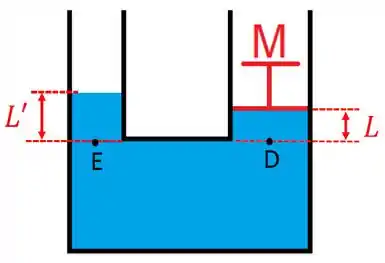
Sabemos que a força peso do objeto de massa empurra o pistão para baixo. Assim, no ponto da figura anterior, temos que a pressão será
sendo a pressão atmosférica, a pressão devido à força peso do objeto de massa e a pressão devido a coluna de fluido de altura .Como a seção reta tem área , então é dado por
Deste modo, temos que
Já no lado esquerdo, temos que a pressão no ponto é somente devido à atmosfera e a coluna de fluido de altura . Assim,
Assim, como os pontos e estão a uma mesma altura da base, então . Logo,
Agora, que calculamos , no próximo passo vamos resolver nosso problema.
Passo 3
Mostramos no passo anterior que
Argumentamos também que
Desta forma,
Portanto,
Passo 4
Analisando todas as alternativas, vemos a que alternativa correta é a letra .
Resposta
.