Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio de Stevin

Ver Teoria
Exercício 20123456789101112131415161718192122232425262728293031323334353637

Enunciado

O recipiente de base retangular mostrado na figura abaixo está cheio de água até a borda. A força que a água faz no fundo, que tem largura d e comprimento L , tem módulo F a . A força total exercida sobre a mesa, subtraindo o peso do recipiente vazio, tem módulo F b . A razão F a   / F b é dada por:

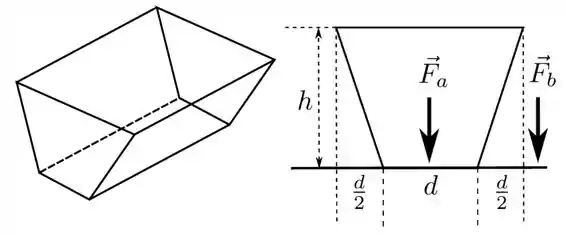
(a) 3/2

(b) 2/3

(c) 1/ 2

(d) 1

Passo 1

Vamos entender primeiro o nosso problema.

A força   F → a é que força que a água emprega somente na base do recipiente. Como ela empurra a base para baixo, a própria base empurra a mesa para baixo com a mesma força. Veja a figura abaixo.

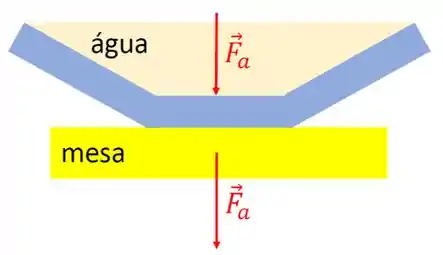
Já a força   F → b é a resultante das forças aplicadas sobre a mesa, subtraindo a força peso do recipiente. Mas vamos pensar um pouco. Em nosso problema, só existem dois corpos: o recipiente e o volume de água. Assim, as forças peso de cada um vai empurrar a mesa para baixo. Veja a figura abaixo.

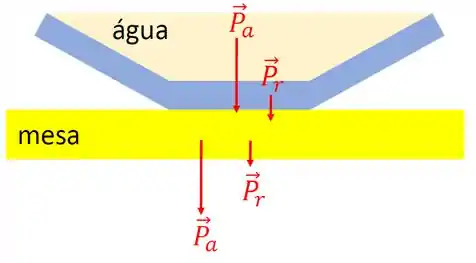
Portanto, podemos afirmar que a força   F → b é na verdade o peso da água, pois, segundo sua definição,

F → b = R e s u l t a n t e s   d a s   f o r ç a s   s o b r e   a   m e s a   -     ( p e s o   d o   r e c i p i e n t e )

F → b = P → a +   P → r - P → r   =   P → a

Agora que entendemos as forças F → a e   F → b , vamos calcular os seus módulos no próximo passo.

Passo 2

Vamos calcular o módulo da força   F → a . Como ela é a força que a água emprega na base do recipiente, então

F a = p b × A b

sendo p b a pressão na base do recipiente e A b a área da base.

Desconsiderando a pressão atmosférica (pois não consideramos a força devido à ela sobre a mesa), a pressão na base do recipiente é dada por

p b =   ρ á g u a × g × h

Já a base do recipiente é um retângulo de largura d e comprimento L . Deste modo,

A b = d × L

Portanto, o módulo da força F → a é igual a

F a =   ρ á g u a × g × h × d × L

Já o módulo da força   F → b é igual ao módulo da força peso da água dentro do recipiente. Assim,

F b = P → a = M á g u a × g

sendo M á g u a a massa de água dentro do recipiente.

Como a densidade da água ( ρ á g u a ) é constante, podemos fazer

M á g u a = ρ á g u a × V á g u a

com V á g u a o volume da água.

O enunciado diz que o recipiente está cheio até a borda. Assim, V á g u a = V r e c i p i e n t e e

V á g u a = V r e c i p i e n t e = A t × L

sendo A t a área da seção reta do recipiente (que é um trapézio). Veja a figura abaixo.

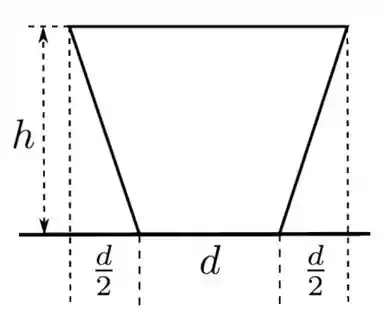
Assim,

A t = b a s e   m a i o r + b a s e   m e n o r × a l t u r a 2

A t = 2 d + d × h 2 = 3 2 × d × h

Logo,

V á g u a = A t × L =   3 2 × d × h × L

Desta forma,

M á g u a =   ρ á g u a × V á g u a =   3 2 × ρ á g u a × d × h × L

E finalmente

F b = M á g u a × g =   3 2 × ρ á g u a × g × d × h × L  

Agora que determinamos os módulos, no próximo passo vamos responder o exercício.

Passo 3

Mostramos no passo anterior que

F a =   ρ á g u a × g × h × d × L                       e                     F b = 3 2 ×   ρ á g u a × g × h × d × L

Desta forma, a razão F a / F b é dada por

F a F b = ρ á g u a × g × h × d × L 3 2 × ρ á g u a × g × h × d × L = 1 3 2 = 2 3

Portanto, a razão F a / F b é igual a 2 / 3 .

Passo 4

Analisando todas as alternativas, vemos a que alternativa correta é a letra ( b ) .

Resposta

L e t r a   ( b ) .

Exercícios de Livros Relacionados

Dois recipientes cilíndricos iguais, com as bases no mesmo nível, contêm um líquido de massa específica 1,30 × 10 ³k g / m ³ . ³ ³ A área de cada base é 4,00c m ² ², mas em um dos recipientes a altura
(Homens e elefantes fazendo snorkel) Quando uma pessoa faz snorkel, os pulmões estão conectados diretamente a atmosfera através do tubo de respiração e, portanto, se encontram a pressão atmosférica. Q
Os cientistas encontraram indícios de que Marte pode ter tido outrora um oceano com 0,500km de profundidade. A aceleração da gravidade em Marte é 3,71 m / s 2 . (a) Qul seria a pressão manométrica no
Um barril contém uma camada de óleo de 0,120m flutuando sobre a água com uma profundidade igual a 0,250m. A densidade do óleo é igual a 600 k g / m 3 . (a) Qual é a pressão manométrica na interface en
A figura mostra um tubo em forma de U modificado: o lado direito é mais curto que o esquerdo. A extremidade do lado direito está d = 10,0c m acima da bancada do laboratório. O raio do tubo é 1,50c m .