Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio de Stevin

Ver Teoria
Exercício 35123456789101112131415161718192021222324252627282930313233343637

Enunciado

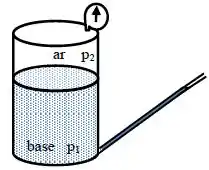
O cilindro mostrado na figura contém ar e água. À sua base superior, com 400 c m 2 de área, encontra-se acoplado um manômetro. Junto à base inferior do cilindro foi conectado um tubo fino aberto para a atmosfera, inclinado de 30 º em relação à horizontal, preenchido com mercúrio até ocupar 50   c m do tubo. Observa-se que a camada de água dentro do cilindro tem 30 c m de altura.

(a) Determine a pressão manométrica na base inferior do cilindro

(b) Determine a leitura do manômetro (pressão manométrica do ar interno)

(c) Calcule a diferença entre as forças de pressão nas bases inferior e superior do cilindro. Compare com o peso da água.

Dados:

ρ m e r = 13,6 × 10 3 k g / m 3

Passo 1

A pressão na base vai ser devido a coluna de mercúrio somada com a pressão atmosférica, já que a coluna de mercúrio está em contato com o ar

p 1 = ρ m e r g h + p a t m

A altura da coluna de mercúrio vai se a altura de um triângulo retângulo de hipotenusa l = 0,5 m (o quanto o mercúrio ocupa o tubo) e com ângulo de 30 º , ou seja

h = l s e n 30 º = l 2

Assim

p 1 = ρ m e r g l 2 + p a t m

Já a pressão manométrica é definida como

p 1 m = p 1 - p a t m

p 1 m = ρ m e r g l 2 = 13,6 × 10 3 × 10 × 0,5 2

p 1 m = 3,4 × 10 4   P a

Passo 2

Não parece, mas esse cilindro é fechado, beleza? Fiquei mó tempão aqui quebrando cabeça pra entender hahaha! Então vamos lá!

A pressão na base vai ser a pressão do ar de dentro somada com a pressão da coluna de água, beleza?

p 1 = p 2 + ρ á g u a g h → p 2 = p 1 - ρ á g u a g h

Já a pressão manométrica

p 2 m = p 2 - p a t m → p 2 = p 2 m + p a t m

Assim

p 2 m + p a t m = p 1 m + p a t m - ρ á g u a g h

p 2 m = p 1 m - ρ á g u a g h

Substituindo os dados do enunciado e p 1 m do passo anterior

p 2 m = 3,4 × 10 4 - 10 3 × 10 × 0,3

p 2 m = 3,1 × 10 4   P a

Passo 3

A força na base inferior será dada por

F i n f = p 1 m A

E na base superior

F s u p = p 2 m A

A diferença de forças será dada por

F i n f - F s u p = p 1 m - p 2 m A = 3,4 × 10 4 - 3,1 × 10 4 × 400 × 10 - 4

Lembrando que 1 c m 2 = 10 - 4 m 2 !

Assim

F i n f - F s u p = 120 N

E qual o peso da água nesse cilindro?

P = V á g u a ρ á g u a g = A b a s e h á g u a ρ á g u a g

P = 400 × 30 × 10 - 6 × 1000 × 10

P = 120   N

Que é exatamente igual à força que encontramos. Repara que aquele 10 - 6 ali surgiu porque eu passei de c m 3 pra m 3 .

Resposta

(a)

p 1 m = 3,4 × 10 4   P a

(b)

p 2 m = 3,1 × 10 4   P a

(c)

F i n f - F s u p = 120 N

Exercícios de Livros Relacionados

Dois recipientes cilíndricos iguais, com as bases no mesmo nível, contêm um líquido de massa específica 1,30 × 10 ³k g / m ³ . ³ ³ A área de cada base é 4,00c m ² ², mas em um dos recipientes a altura
(Homens e elefantes fazendo snorkel) Quando uma pessoa faz snorkel, os pulmões estão conectados diretamente a atmosfera através do tubo de respiração e, portanto, se encontram a pressão atmosférica. Q
Os cientistas encontraram indícios de que Marte pode ter tido outrora um oceano com 0,500km de profundidade. A aceleração da gravidade em Marte é 3,71 m / s 2 . (a) Qul seria a pressão manométrica no
Um barril contém uma camada de óleo de 0,120m flutuando sobre a água com uma profundidade igual a 0,250m. A densidade do óleo é igual a 600 k g / m 3 . (a) Qual é a pressão manométrica na interface en
A figura mostra um tubo em forma de U modificado: o lado direito é mais curto que o esquerdo. A extremidade do lado direito está d = 10,0c m acima da bancada do laboratório. O raio do tubo é 1,50c m .