Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio de Stevin

Ver Teoria
Exercício 17123456789101112131415161819202122232425262728293031323334353637

Enunciado

A área do topo do cilindro da figura mede 2 m2 e sobre ela encontra-se acoplado um manômetro. O cilindro é preenchido por ar, óleo e água. As camadas de óleo e água têm 10 cm e 20 cm de altura, respectivamente. Junto à base do cilindro foi conectado um tubo, inclinado 30° em relação à horizontal e aberto para a atmosfera, ocupado por água conforme mostrado na figura. Determine:

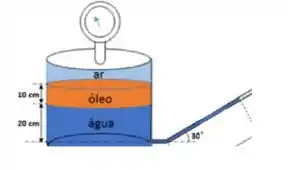
Dados: ρ á g u a = 1000 k g m 3 ; ρ ó l e o = 800 k g m 3 ;   ρ a r = 1,21 k g m 3 ; comprimento do tubo L = 60 cm.

a) A leitura do manômetro.

b) A força exercida pelo ar apenas sobre a superfície interna do topo do cilindro;

c) A força exercida pela água sobre o fundo do cilindro.

Passo 1

a) Repare aqui que ele tá pedindo a pressão manométrica! Essa pressão vai ser a pressão do ar no interior do cilindro menos a pressão atmosférica, ou seja:

p m a n o m é t r i c a = p a r - p a t m

Como nós vamos achar isso?

O comprimento daquele tubo inclinado é de 60 cm. Vamos achar a altura vertical da coluna de água.

h = L s e n 30 0 = 60 × 1 2 = 30   c m

Vê bem, essa altura é igualzinha à altura da água + óleo dentro do cilindro.

Passo 2

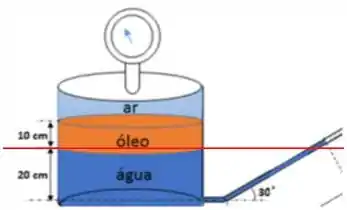
Vou igualar agora a pressão na interface água/óleo com a pressão na mesma altura dentro do tubo inclinado:

p ó l e o + p a r = p á g u a + p a t m

Dá uma olhada na figura, eu to fazendo a pressão nessa linha vermelha:

Rearranjando:

p a r - p a t m = p á g u a - p ó l e o

E isso aí que apareceu do lado esquerdo é o que eu quero encontrar!

p a r - p a t m = ρ á g u a g h á g u a - ρ ó l e o g h ó l e o

p a r - p a t m = 1000 × 10 × 0,1 - 800 × 10 × 0,1

p a r - p a t m = 200   P a

Passo 3

b) Vamos achar a pressão exercida pelo ar:

p a r - p a t m = 200   P a

p a r = 200 + 1,01 × 10 5

Eita! Mas tá vendo que esse 200 é muito, muito, muiiiiito pequeno perto do 10 5 ? Então a gente dá uma desconsiderada nesse cara, e fica:

p a r = 1,01 × 10 5   P a

Como:

p = F A

F = p A = 1,01 × 10 5 × 2

F = 2,02 × 10 5   N

Passo 4

c) A força exercida pela água no fundo do cilindro vai ser:

F á g u a = p f u n d o A

Para achar a pressão no fundo, podemos calcular a pressão no tubo inclinado à mesma altura vertical. Que vai ser a mesma e vai dar menos trabalho.

A pressão no fundo do tubo vai ser então:

p f u n d o = p á g u a + p a t m

p f u n d o = ρ á g u a g h + 1,01 × 10 5

p f u n d o = 1000 × 10 × 0,3 + 1,01 × 10 5

p f u n d o = 1,04 × 10 5   P a

Substituindo na força:

F á g u a = 1,04 × 10 5 × 2

F á g u a = 2,08 × 10 5   N

Resposta

a) p a r - p a t m = 200   P a

b) F = 2,02 × 10 5   N

c) F á g u a = 2,08 × 10 5   N

Exercícios de Livros Relacionados

Dois recipientes cilíndricos iguais, com as bases no mesmo nível, contêm um líquido de massa específica 1,30 × 10 ³k g / m ³ . ³ ³ A área de cada base é 4,00c m ² ², mas em um dos recipientes a altura
(Homens e elefantes fazendo snorkel) Quando uma pessoa faz snorkel, os pulmões estão conectados diretamente a atmosfera através do tubo de respiração e, portanto, se encontram a pressão atmosférica. Q
Os cientistas encontraram indícios de que Marte pode ter tido outrora um oceano com 0,500km de profundidade. A aceleração da gravidade em Marte é 3,71 m / s 2 . (a) Qul seria a pressão manométrica no
Um barril contém uma camada de óleo de 0,120m flutuando sobre a água com uma profundidade igual a 0,250m. A densidade do óleo é igual a 600 k g / m 3 . (a) Qual é a pressão manométrica na interface en
A figura mostra um tubo em forma de U modificado: o lado direito é mais curto que o esquerdo. A extremidade do lado direito está d = 10,0c m acima da bancada do laboratório. O raio do tubo é 1,50c m .