Um tubo em U simples contém mercúrio. Quando de água são derramados no ramo esquerdo, a que altura sobe o mercúrio no lado direito, com relação ao seu nível inicial?
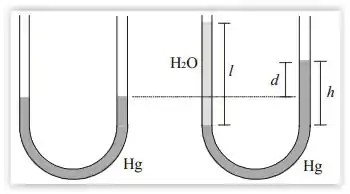
Considere
Passo 1
Pela figura, queremos descobrir a distância , isto é, a diferença entre a nova altura do mercúrio no lado direito com relação ao nível inicial, ilustrado na primeira figura.
Para isso, aplicamos o Princípio de Stevin: igualamos as pressões de um mesmo fluido a uma mesma altura.
Neste caso, vamos igualar as pressões nos pontos (1) e (2), que correspondem à interface entre os fluidos no lado esquerdo e o ponto correspondente no lado direito:
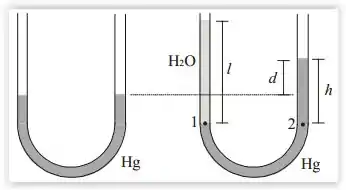
Logo:
Passo 2
Vamos calcular as pressões e :
Calculando :
onde , conforme o enunciado falou, e é a densidade da água:
Calculando :
onde é a densidade do mercúrio.
Passo 3
Igualando as pressões:
Passo 4
Substituindo os valores:
Passo 5
Agora, para calcular , temos que parar um segundo pra perceber uma coisa:
A quantidade total de mercúrio é fixa!
Ou seja: o mercúrio se deslocou mas a quantidade total de fluido não se alterou. Portanto, tudo o que desce no lado esquerdo, necessariamente tem que subir no lado direito!
Pois estamos supondo, também, que o líquido não se comprime nem se distende, ou seja, é um líquido incompressível:
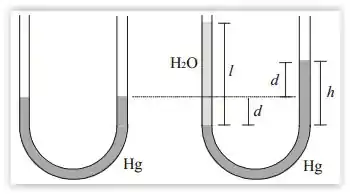
Percebeu?
Se o líquido sobe no lado direito, então ele desceu no lado esquerdo.
Pela figura, podemos ver então o seguinte:
Pronto! Como já calculamos , agora ficou fácil: