Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio de Stevin

Ver Teoria
Exercício 21123456789101112131415161718192022232425262728293031323334353637

Enunciado

Física Termodinâmica e Ondas – Young e Freedman – 12 edição – Capítulo 14 – Exercício 23.

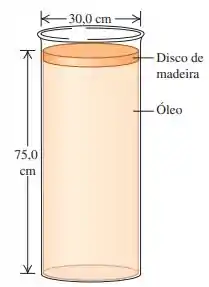
(Cap 14 - Ex 23) Um disco cilíndrico de mandeira, pesando 45,0 N e co um diâmetro de 30,0 cm, flutua sobre um cilindro de óleo de densidade 0,850 g / c m 3 (Figura 14.34). O cilindro de óleo está a 75,0cm de profundidade e tem o mesmo diâmetro que o disco de madeira. (a) Qual é a pressão manométrica no topo da coluna de óleo? (b) Suponha agora que algém coloque um peso de 83,0N sobre a madeira, e que nenhum óleo passe pela beirada do disco de madeira. Qual é a variação de pressão (i) no fundo do cilindro de óleo e (ii) na metade do cilindro do óleo?

Passo 1

Falai meus amores, bora pra mais uma?

A pressão manométrica relacionada ao pesso ( w ) e a área ( A ) do objeto é

p - p 0 = w A    

Portanto, a pressão do manômetro na parte superior da coluna de óleo deve produzir uma força no disco igual ao seu peso.

A área da parte inferior do disco é

A = π r 2 = π 0,150 m 2 = 0,0707 m 2

Passo 2

  1. a pressão manométrica no topo da coluna de óleo é dada por

    2. p - p 0 = w A = 45 N 0,0707 m 2

    p - p 0 = 636 P a

    Passo 3

  2. O aumento da pressão produz uma força no disco igual ao aumento do peso. Pela lei de Pascal, o aumento da pressão é transmitido a todos os pontos do óleo.

∆ p = 83 N 0,0707 m 2 = 1170 P a

  1. No fundo do cilindro de óleo e de 1.17 × 10 3 P a

  2. Na metade do cilindro do óleo, de acordo com a lei de Pascal, o aumento da

pressão é o mesmo em todos os pontos do óleo.

Portanto, a mudança na pressão na metade do óleo é 1.17 × 10 3 P a .

A pressão absoluta no topo do óleo produz uma força para cima no disco, mas essa força é

parcialmente equilibrado pela força devido à pressão do ar na parte superior do disco.

Resposta

  1. 636 P a
  2. (i) 1170 P a   (ii) 1170 P a

Exercícios de Livros Relacionados

Dois recipientes cilíndricos iguais, com as bases no mesmo nível, contêm um líquido de massa específica 1,30 × 10 ³k g / m ³ . ³ ³ A área de cada base é 4,00c m ² ², mas em um dos recipientes a altura
(Homens e elefantes fazendo snorkel) Quando uma pessoa faz snorkel, os pulmões estão conectados diretamente a atmosfera através do tubo de respiração e, portanto, se encontram a pressão atmosférica. Q
Os cientistas encontraram indícios de que Marte pode ter tido outrora um oceano com 0,500km de profundidade. A aceleração da gravidade em Marte é 3,71 m / s 2 . (a) Qul seria a pressão manométrica no
Um barril contém uma camada de óleo de 0,120m flutuando sobre a água com uma profundidade igual a 0,250m. A densidade do óleo é igual a 600 k g / m 3 . (a) Qual é a pressão manométrica na interface en
A figura mostra um tubo em forma de U modificado: o lado direito é mais curto que o esquerdo. A extremidade do lado direito está d = 10,0c m acima da bancada do laboratório. O raio do tubo é 1,50c m .