Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio de Stevin

Ver Teoria
Exercício 31245678910111213141516171819202122232425262728293031323334353637

Enunciado

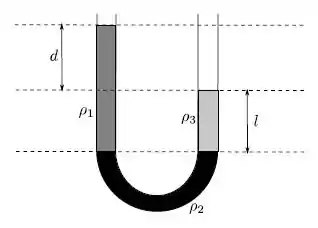
Em um tubo em U, com ambas as extremidades abertas para a atmosfera, coloca-se cuidadosamente três líquidos de densidades diferentes ρ 1 , ρ 2 e ρ 3 , de forma que estes não se misturam. Após o equilíbrio ser atingido, a disposição dos líquidos é a ilustrada na figura. A relação entre as densidades dos líquidos 1 e 3 é:

  1. ρ 1 =   l l   +   d ρ 3
  2. ρ 1 =   l d ρ 3
  3. ρ 1 =   l   +   d l ρ 3
  4. ρ 1 =   l l   -   d   ρ 3

Passo 1

Vamos usar o princípio de Stevin aqui: A pressão na interface dos líquidos de densidades ρ 1 e ρ 3 com o ar atmosférico deve ser a mesma já que estão sob a pressão atmosférica.

Outro detalhe importante é presença do fluido ρ 2 . O princípio de Stevin diz que devemos fazer comparações em um mesmo fluido, não é mesmo?

Pois bem, se compararmos as pressões nas interfaces dos líquidos, estaremos fazendo a comparação de pressões no mesmo líquido: ρ 2 , já que ele possui duas interfaces: uma com ρ 1 e outra com ρ 3 .

Passo 2

Beleza. A pressão devido à ρ 1 é dada por:

p 1 = ρ 1 d + l g

E a pressão causada por ρ 3 é dada por:

p 3 = ρ 3 l g

Como:

p 1 = p 3

Temos que:

ρ 1 d + l g = ρ 3 l g → ρ 1 = l l   +   d ρ 3

Resposta

a)

Exercícios de Livros Relacionados

Dois recipientes cilíndricos iguais, com as bases no mesmo nível, contêm um líquido de massa específica 1,30 × 10 ³k g / m ³ . ³ ³ A área de cada base é 4,00c m ² ², mas em um dos recipientes a altura
(Homens e elefantes fazendo snorkel) Quando uma pessoa faz snorkel, os pulmões estão conectados diretamente a atmosfera através do tubo de respiração e, portanto, se encontram a pressão atmosférica. Q
Os cientistas encontraram indícios de que Marte pode ter tido outrora um oceano com 0,500km de profundidade. A aceleração da gravidade em Marte é 3,71 m / s 2 . (a) Qul seria a pressão manométrica no
Um barril contém uma camada de óleo de 0,120m flutuando sobre a água com uma profundidade igual a 0,250m. A densidade do óleo é igual a 600 k g / m 3 . (a) Qual é a pressão manométrica na interface en
A figura mostra um tubo em forma de U modificado: o lado direito é mais curto que o esquerdo. A extremidade do lado direito está d = 10,0c m acima da bancada do laboratório. O raio do tubo é 1,50c m .