Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio de Stevin

Ver Teoria
Exercício 23123456789101112131415161718192021222425262728293031323334353637

Enunciado

Física Termodinâmica e Ondas – Young e Freedman – 12 edição – Capítulo 14 – Exercício 16.

(Cap 14 - Ex 16) O líquido no manômetro de tubo aberto indicadi na Figura 14.9a é o mercúrio, y 1 = 3,0 c m e y 2 = 7,0   c m . A pressão atmosférica é igual a 980milibares. a) Qual é a pressão absoluta no fundo do tubo em forma de U? b) Qual é a pressão absoluta no tubo aberto a uma profundidade de 4,0cm abaixo da superfície livre? c) Qual é a pressão absoluta do gás no tanque? d) Qual é a pressão manométrica do gas em pascals?

Passo 1

Falai galerinha, show de bola?

Bom, iremos usar a seguinte equação

p = p 0 + ρ g h

para calcular a pressão nas profundidades especificadas no tubo aberto.

O liquido no manômetro de tubo aberto recebe os seguintes dados

y 1 = 3.00   c m = 3.00 × 10 - 2 m

y 2 = 7.00   c m = 7.00 × 10 - 2 m

Para uma melhor visualização iremos utilizar o seguinte diagrama

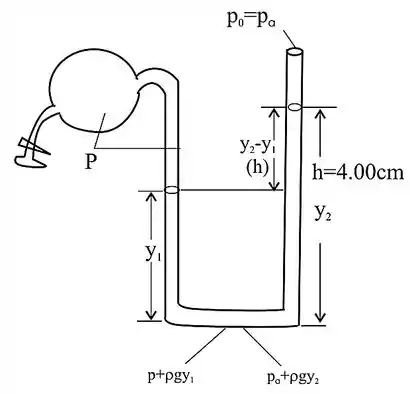
A pressão é a mesma em todos os pontos, a mesma distância do fundo dos tubos, portanto a pressão calculada na parte b é a pressão no tanque.

Pressão manométrica é a diferença entre a pressão absoluta e a pressão do ar.

Note que temos a pressão atmosférica em milibar, precisamos fazer a conversão

p a = 980 m i l i b a r e s = 9,80 × 10 4   P a

Passo 2

  1. Então, aplicando a formula

    2. p = p 0 + ρ g h

    para o tubo direito. A parte superior deste tubo está aberta ao ar, então   p 0 = p a . A densidade do líquido (mercúrio) é 13,6 × 10 3   k g / m 3 .

    Então

    P = P a + ρ g y 2

    p = 9,80 × 10 4 P a + 13,6 × 10 3 k g m 3 9,80 m s 2 0,0700 m

    = 1,07 × 10 5 P a

    Passo 3

  2. E a pressão absoluta do gás no tanque é dada por

    3. P = P a + ρ g y 2

    p = p 0 + ρ g h = 9,80 × 10 4 P a + 13,6 × 10 3 k g m 3 9,80 m s 2 0,0400 m

    = 1,03 × 10 5 P a

    Passo 4

  3. Desde que

    4. P - P a = ρ g h

    Onde

    H = y 2 - y 1

    Portanto, a pressão na superfície do mercúrio no tubo terminal esquerdo é igual à calculada na

    parte (b). Assim, a pressão absoluta do gás no tanque é de

    p = p 0 + ρ g h = 9,80 × 10 4 P a + 13,6 × 10 3 k g m 3 9,80 m s 2 0,0400 m

    1,03 × 10 5 P a

    Passo 5

  4. E a pressão manométrica do gás em pascals é dada por

p - p 0 = ρ g h = ( 13,6 × 10 3 k g / m 3 ( 9,80 m / s 2 ) ( 0,0400 m ) = 5,33 × 10 3   P a

Passo 3

Fazendo uma breve avaliação do exercício, podemos notar que:

Se a equação

p - p a t m = ρ g y 2 - y 1 = ρ g h

for avaliada com a densidade de mercúrio e p - p a = 1 a t m = 1,01 × 10 5   P a , então h = 76   c m .

As colunas de mercúrio aqui são muito menores que 76   c m , portanto, as pressões do manômetro são muito menores que 1,0 × 10 5   P a

P - P a = 13,6 × 10 3 K g / m 3 9.80   m / s 2 0,0400 m

= 5,38 × 10 3 P a

Resposta

  1. 1,07 × 10 5 P a
  2. 1,03 × 10 5 P a
  3. 1,03 × 10 5 P a
  4. 5,38 × 10 3   P a

Exercícios de Livros Relacionados

Dois recipientes cilíndricos iguais, com as bases no mesmo nível, contêm um líquido de massa específica 1,30 × 10 ³k g / m ³ . ³ ³ A área de cada base é 4,00c m ² ², mas em um dos recipientes a altura
(Homens e elefantes fazendo snorkel) Quando uma pessoa faz snorkel, os pulmões estão conectados diretamente a atmosfera através do tubo de respiração e, portanto, se encontram a pressão atmosférica. Q
Os cientistas encontraram indícios de que Marte pode ter tido outrora um oceano com 0,500km de profundidade. A aceleração da gravidade em Marte é 3,71 m / s 2 . (a) Qul seria a pressão manométrica no
Um barril contém uma camada de óleo de 0,120m flutuando sobre a água com uma profundidade igual a 0,250m. A densidade do óleo é igual a 600 k g / m 3 . (a) Qual é a pressão manométrica na interface en
A figura mostra um tubo em forma de U modificado: o lado direito é mais curto que o esquerdo. A extremidade do lado direito está d = 10,0c m acima da bancada do laboratório. O raio do tubo é 1,50c m .