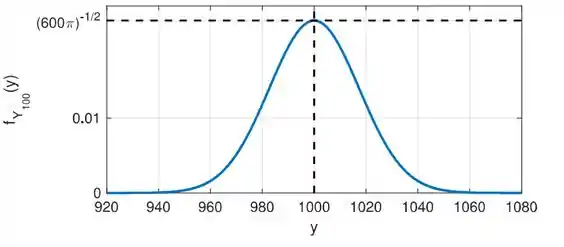
14) A variável aleatória é obtida a partir da soma de variáveis aleatórias independentes, todas com distribuição uniforme em (ou seja, . Y=Uma aproximação para a função densidade de probabilidade de é mostrada na figura ao lado. Os valores de e são respectivamente iguais a:
a) e
b) e
c) e
d) e
e) e
Passo 1
Faaaala galera, quem tá animado pra matar mais uma questão de probabilidade?
Nesse exercício temos uma variável aleatória que é resultado da soma de outras variáveis aleatórias, que possuem distribuição uniforme em um intervalo . O enunciado também dá a função de densidade de probabilidade de , que curiosamente tem a forma de um sino (por que será né?!).
O objetivo é determinarmos e . Beleza?

O problema todo é que a gente só sabe a distribuição das variáveis , mas a função de densidade que temos é da variável . Será que tem alguma forma de saber a distribuição de ?

Pô, o formato da curva já entrega um pouco. Realmente segue uma distribuição normal, isso ocorre por causa do nosso Teorema do Limite Central (TCL).
Segundo esse teorema, a distribuição da média de uma amostra de variáveis aleatórias se aproxima de uma distribuição normal (ficando cada vez mais fiel à medida que o tamanho da amostra aumenta). Daí, podemos afirmar que:
Excelente! Conseguiu entender bem?
Passo 2
Tá beleza, tudo lindo até aqui, mas como é que isso vai nos ajudar a encontrar e ?
É que, como segue uma distribuição uniforme, sabemos que:
Além disso, como foi dada a função de densidade de probabilidade de , e agora sabemos que segue uma distribuição normal, podemos tirar algumas conclusões sobre o seu gráfico:
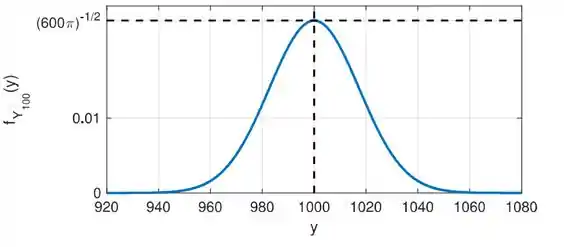
A primeira delas é que o valor central de , ou seja, representa a média da distribuição, .
Um outro negócio massa é lembrar da lei da função densidade de probabilidade na distribuição normal.
Logo, quando , temos:
Só que pelo gráfico, vemos que . Daí, igualando as duas equações, vem:
Logo:
Perfeito!
Passo 3
Agora que já descobrimos os valores de , podemos usar as equações lá do passo :
Substituindo os dados, temos:
Sabemos também que:
Substituindo novamente, vem:
Fazendo agora , descobrimos :
Substituindo esse resultado em , ficamos com:
Prontinho! Matamos mais uma questão!
Espero que vocês tenham entendido bem direitinho, valeu galera 😊
Resposta
Letra b: e .