Analisando a disposição dos vetores BA, EA, CB, CD e DE, conforme figura a seguir, assinale a alternativa que contém a relação vetorial correta:
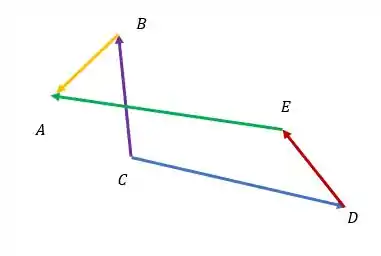
a) CB + CD + DE = BA + EA
b) BA + EA + CB = DE + CD
c) EA – DE + CB = BA + CD
d) EA – CB + DE = BA – CD
e) BA – DE – CB = EA + CD
Passo 1
Pra gente resolver essa parada vamos analisar o caminho percorrido pra chegar de um ponto ao outro e após isso analisar quais caminhos são iguais.
Por exemplo, temos dois jeitos de sair de para .
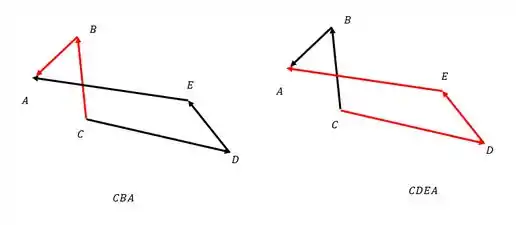
Podemos fazer o percurso ou o percurso e em ambos os percursos o deslocamento resultante será de para .
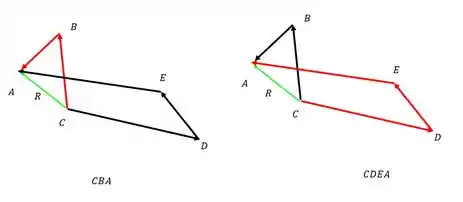
É como quando pegamos um caminho mais longo pra chegar no mesmo local, mesmo que o percurso seja maior o resultado final é o mesmo pois acabamos andando no sentido oposto do que se queria chegar.
Passo 2
Conhecendo agora que esses percursos são iguais pois saem do mesmo ponto e chegam num mesmo ponto, podemos escrever isso do jeito que a questão nos pede.
Putz mas não tem essa resposta lá, e agora?

Fica tranquilo, essa resposta tem lá sim só que não tá no formato certo das alternativas, vamos analisar.
a) CB + CD + DE = BA + EA
b) BA + EA + CB = DE + CD
c) EA – DE + CB = BA + CD
d) EA – CB + DE = BA – CD
e) BA – DE – CB = EA + CD
Temos que ter aqui e com sinais opostos isso não ocorre na alternativa b nem c e nem na alternativa e, sobrando só pra gente as alternativas a e d. Olhando pra alternativa a temos e no mesmo lado com mesmo sinal, o que não acontece na nossa igualdade.
Nossa vencedora então é a alternativa d, e pra chegarmos nela é só passar pra um lado e pro outro.
E trocar os lados né já que essa alternativa maluca inverteu tudo pra confundir ainda mais a nossa cabeça.