USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I, Questão 17f
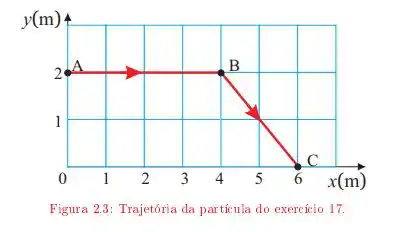
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:
f. O tempo que a partícula leva para sair de A e chegar em C;
Passo 1
Eaew, belezinha?
Temos que encontrar o tempo que a partícula leva para sair de A e chegar em C. Temos uma relação para esse tempo em termos da distância percorrida e a velocidade.
Vamos lá!
Passo 2
Temos que o tempo é dado pela razão entre a distância percorrida e o módulo da velocidade constante :
.
Passo 3
Olhando para a trajetória no trecho AB, a distância percorrida é igual a . Já na trajetória BC, essa distância é dada pela relação de Pitágoras:
Passo 4
Então, como o módulo da velocidade é constante em todo percurso, temos que o tempo total será
.
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
.