USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 27a
Uma partícula percorre, com velocidade constante e no sentido anti-horário, uma circunferência de raio igual a e completa uma volta em segundos. A partícula passa pelo ponto em . Tomando a origem em , de acordo com a figura , determine:
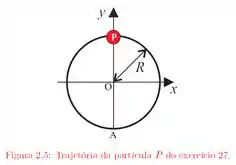
(a) O módulo e a direção dos vetores que descrevem sua posição , e segundos mais tarde;
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente verificar as coordenadas do vetor posição quando a partícula parte do ponto , em , e, percorrendo a circunferência no sentido anti-horário, chega em , e .
Pra isso, vamos precisar extrair as informações do raio, , e do perído, , dados pelo enunciado. Dessa forma, sabendo que a partícula percorreu uma fração do período, , podemos encontrar o valor do ângulo percorrido e usar as relações trigonométricas:
para achar as coordenadas do vetor posição naquele instante.
Vamos lá!
Passo 2
A partícula percorre um determinado tempo em relação ao período total que ela leva para dar uma volta. Então, para , temos:
Assim, o ângulo descrito pela partícula pode ser dado pela relação:
Podemos verificar as coordenadas do ponto, usando e fazendo:
Sendo assim, em , temos ou, na forma vetorial:
Passo 3
Para , temos:
Assim, o ângulo descrito pela partícula pode ser dado pela relação:
Podemos verificar as coordenadas do ponto, usando e fazendo:
Sendo assim, em , temos ou, na forma vetorial:
Passo 4
Para , temos:
Assim, o ângulo descrito pela partícula pode ser dado pela relação:
Podemos verificar as coordenadas do ponto, usando e fazendo:
Sendo assim, em , temos ou, na forma vetorial:
Valeu, galera! Até a próxima! 😉