UFABC – Fundamentos de Mecânica – Lista 1 – Questão 2
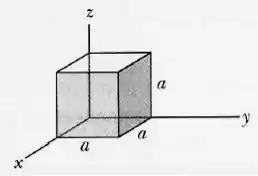
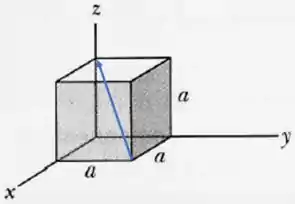
(a) Na Figura abaixo, um cubo de lado a tem um de seus vértices posicionado na origem de um sistema de coordenadas xyz. Uma diagonal de centro é uma linha que vai de um vértice a outro passando pelo centro. Em termos dos vetores unitários, qual é a diagonal de centro que se estende a partir do vértice nas coordenadas (x; y; z) iguais a
(a) (0; 0; 0);
(b) (a; 0; 0);
(c) (0; a; 0),
(d) (a; a; 0)?
(e) Determine os ângulos que as diagonais de centro fazem com os lados adjacentes.
(f) Determine o comprimento das diagonais de centro em função de a.
Passo 1
Oi, tudo bem? Essa questão parece confusa, mas vou te ajudar! Vem comigo! Nos primeiros itens precisamos identificar qual é o ponto de vértice oposto ao dado. Bom, precisamos achar o ponto mais distante do dado (passando pelo centro) e calcular o vetor. Em cada caso vamos ver que com um desenho tudo se resolve!
E nos dois últimos itens o problema pede para calcularmos os ângulos das diagonais com os lados. Bom, nessas vamos aplicar as relações de seno e cosseno de um triângulo retângulo (afinal, relembrar é viver!)
Mas relaxa, vou fazer com você!
Vamos lá?
Passo 2
- Vamos encontrar o vértice oposto ao ponto (0,0,0), sempre passando pelo centro do cubo, olha só como fica no desenho:
- O ponto inicial que queremos é (a,0,0). Pelo desenho vemos que o extremo oposto é o ponto (0,a,a):
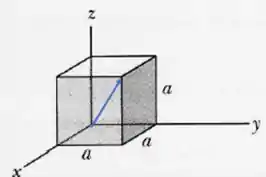
O ponto (a,a,a) é o mais distante, o ponto inicial é (0,0,0) então a diagonal é o vetor que vai do ponto final menos o inicial:
Beleza? Agora vamos repetir isso para os outros pontos!
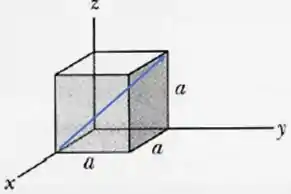e a diagonal é a diferente entre os pontos final e inicial:
Certo?
A ideia é repetir para todos os outros pontos! Vamos lá?
Passo 3
Letra (c): o ponto que estamos agora é o (0,a,0). Pelo desenho, o ponto oposto é o (a,0,a):
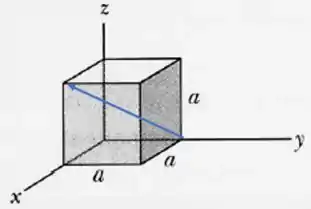
E sua diagonal é:
Beleza? E por fim (ufa!) o último ponto dado é o da letra (d): (a,a,0). Seu vértice oposto é o (0,0,a):
E sua diagonal:
Tranquilo? Vamos para os ângulos?
Passo 4
Letra (e):
Agora o problema pede o ângulo entre as diagonais de centro com os lados adjacentes! Bom, essas diagonais são a das faces (como se fosse a diagonal da base, por exemplo) com a diagonal do cubo (do ponto da origem até o ponto (a,a,a) por exemplo). Vou desenhar essas duas diagonais e você vai ver que elas formam um triângulo bem conhecido:
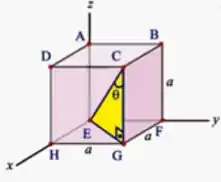
A diagonal da base inferior é o segmento , que é a diagonal de um quadrado: . Já a diagonal do cubo é o segmento . E para determinar o ângulo podemos usar a função seno:
Beleza? Vamos para o último item?
Passo 5
Letra (f): agora por fim queremos saber o ângulo em função do lado a. Mas isso nós já achamos! A diagonal da base é e do cubo é !
E é isso!
Espero ter ajudado!