Um explorador caminha para leste, a partir do acampamento, vira então para a esquerda e caminha sobre um arco de círculo centrado no acampamento e, finalmente, caminha mais direto para o acampamento. A que distância o explorador está do acampamento ao fim dessa caminhada? Qual a orientação da posição do explorador em relação ao acampamento? Qual é a razão entre a magnitude final do deslocamento e a distância total caminhada?
Passo 1
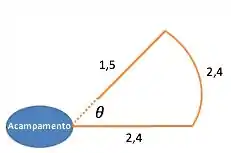
O primeiro passo é desenhar grosseiramente o movimento que o explorador fez, para conseguirmos analisar melhor o movimento que ele fez.
O movimento deve ser algo parecido com isso
Passo 2
Resolver esse item é necessário ter uma “sacada” não muito trivial.
Ao final de andar os primeiros para leste o explorador começa a caminhar sobre um arco de círculo centrado no acampamento.
Se o centro do círculo é o acampamento, não importa se ele andou sobre o círculo ou , quando ele parar de andar, sua distância em relação ao acampamento será a mesma de quando ele começou, pois será o raio do círculo, que foi determinado pelos primeiros andados.
Então quando ele termina de andar os sobre o círculo centrado no acampamento, ele está a do acampamento. Como o explorador anda diretamente para o acampamento, significa que sua distância para o acampamento é:
Passo 3
Para sabermos a orientação do explorador, precisamos saber quantos graus equivalem aos andados sobre o círculo. Para assim sabermos em qual posição o explorador parou.
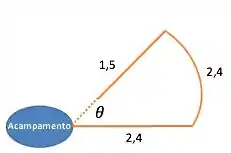
Vamos fazer uma regra de três para descobrir o valor do ângulo.
Sabemos que equivale a , assim:
Temos que o vetor posição do explorador está a acima do eixo leste.
Passo 4
O deslocamento já calculamos e vimos que , a distância percorrida é a soma dos quando ele andou e por isso temos :
Fazendo a Razão do deslocamento final, com a distância percorrida, chegamos em:
Resposta
O vetor posição do explorador está a acima do eixo leste.