Cinemática Tridimensional
Dois carros e (considerados como partículas) partem da mesma posição no instante e percorrem estradas perpendiculares, seguindo para o norte e o leste, respectivamente, com velocidades contantes e . A distância entre os dois carros no instante satisfaz à relação:
Passo 1
Ambos os movimentos possuem velocidade constante. Isso quer dizer que ambos são movimentos uniformes. Vamos dizer que os dois partem da origem, então os dados do problema são
A posição de A, que varia ao longo do , ao longo do tempo será
Passo 2
A posição de B, que varia ao longo do , ao longo do tempo será
Passo 3
Vamos fazer um esboço de como são esses movimentos.
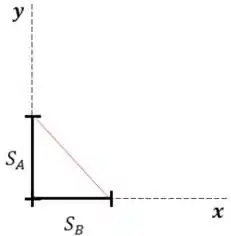
Repare que a distância entre eles é a hipotenusa do triângulo retângulo então usando o teorema de Pitágoras
Resposta
Letra C
Exercícios de Livros Relacionados
O oásis A está 90k m a oeste do oásis B . Um camelo parte de A e leva 50h para caminhar 75k m na direção 37 ° ao norte do leste. Em seguida, leva 35h para caminhar 65k m para o sul e descansa por 5,0h
Na Fig. 4-49, uma estação de radar detecta um avião que se aproxima, vindo do Leste. Quando é observado pela primeira vez, o avião está a uma distância d 1 = 360m da estação e θ 1 = 40 ° acima do hori
Mostre que uma pedra atirada para cima leva o mesmo tempo na subida e na descida.
O vetor posição de um próton é inicialmente r →=5,0 i →- 6,0 j →+ 2,0 k → e depois se torna r → =- 2,0 i →+6,0 j →+ 2,0 k → , com todos os valores em metros. (a) Qual é o vetor deslocamento do próton?
Na cobrança do pênalti, no jogo de futebol, a bola é chutada à distância de 11m do gol, e a velocidade típica da bola é 100k m / h . O tempo que o goleiro gasta pra cair é aproximadamente igual ao tem