Um esquiador percorre com ângulo de considerando rotação em sentido do sul para o oeste, a seguir a em sentido do leste para o norte, e finalmente a em sentido do oeste para o sul. Qual a distância entre o início e fim do trajeto.
Dados:
Passo 1
Para calcular a distância entre o início e o final devemos achar o deslocamento vetorial desse esquiador. Vamos considerar o início saindo da origem.
Primeiro ele percorre com ângulo de considerando rotação em sentido do sul para o oeste. Vamos ver uma figura para ver como isso fica.
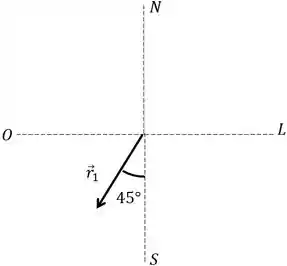
Passo 2
Vamos achar agora suas componentes usando a “regra do COlado/SEparado”
O deslocamento fica
Passo 3
Vamos agora achar o segundo deslocamento, fazendo de novo uma figura para ajudar.
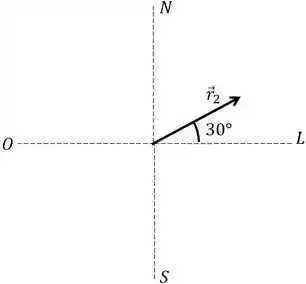
Vamos achar agora suas componentes usando a “regra do COlado/SEparado”
O deslocamento fica
Passo 4
Vamos agora achar o terceiro trecho.
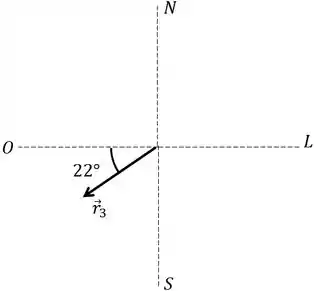
Vamos achar agora suas componentes usando a “regra do COlado/SEparado”
O deslocamento fica
Passo 5
O total vai ser
Passo 6
A distância entre o início e o fim é o módulo do vetor deslocamento total.