Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Vetor Deslocamento

Ver Teoria
Exercício 10123456789111213141516171819202122232425262728293031323334

Enunciado

UNICAMP 2020.1 - Física Geral 2

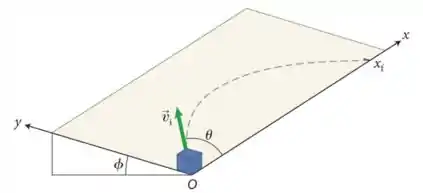
Um bloco de inércia m está localizado na origem de um sistema de coordenadas x y alinhado em relação a um plano inclinado que faz um ângulo ϕ em relação a horizontal (ver a figura abaixo). Você lança um bloco ao longo da inclinação, com velocidade inicial v i fazendo um ângulo θ com o eixo x do plano inclinado.

a) Qual é o módulo e a direção da aceleração do bloco expressa no sistema de coordenadas indicado na figura?

b) Derive a expressão para a velocidade do bloco em função do tempo, expressa em notação vetorial para o sistema de coordenadas indicado.

c) Qual é o valor máximo do deslocamento do bloco, ∆ y , ao longo do eixo y ?

d) Qual é o máximo deslocamento do bloco, ∆ x , ao longo do eixo x . Ignore o atrito e qualquer outra dissipação.

e) Discuta seus resultados nas situações extremas ϕ   =   0 ° e ϕ   =   90 °

Passo 1

(a) Como costumeiramente estão costumados, nossa gravidade aponta para o centro da Terra, a não ser que você seja Terraplanista e não creia na gravidade, mas não é o ponto aqui. Então como o plano apresenta uma inclinação ϕ , temos que

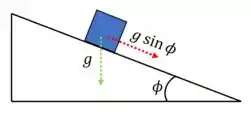
Quando o bloco caminha pelo pontilhado, ele sente a gravidade decomposta, ou seja

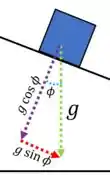
Assim temos que a aceleração que o bloco sente será

a → = - g sin ⁡ ϕ   j →

Passo 2

(b) Agora analisando nossa velocidade, na direção x temos que ela é constante e vale

v x ( t ) = v i cos ⁡ θ

Enquanto na direção y , podemos encontrar pela aceleração determinada acima, ou seja

d d t v ≡ a = - g sin ⁡ ϕ

Integrando em ambos os lados em t , espero que já aprendemos integrais simples... teremos que

∫ d d t v d t = - ∫ g sin ⁡ ϕ   d t

Que não se engane, não são integrais indefinidas, nos sabemos os limites de integração, ou seja

∫ v i sin ⁡ θ v y t d d t v   d t = - ∫ 0 t g sin ⁡ ϕ   d t

Pelo teorema fundamental do cálculo, a primitiva da derivada é a própria função, ou seja

v y t - v i sin ⁡ θ = - g t sin ⁡ ϕ

Assim temos que

v y t = v i sin ⁡ θ - g t sin ⁡ ϕ

Assim temos que

v → = v i cos ⁡ θ i → + v i sin ⁡ θ - g t sin ⁡ ϕ j →

Passo 3

(c) Assim como resolveríamos esse problema em um lançamento vertical, o deslocamento máximo na direção y ocorre exatamente no momento que tivéssemos

d d t y = 0

Não vejo porque aqui deveria ser diferente. Olhando para o nosso deslocamento na figura do enunciado, temos que o mesmo caso acontece para nosso problema. Assim tome que

v y ≡ d d t y = v i sin ⁡ θ - g t sin ⁡ ϕ = 0

O que implica que o tempo que o bloco leva para chegar a altura máxima é

t m a x = v i sin ⁡ θ g sin ⁡ ϕ

Assim como em um lançamento obliquo, que teríamos

y t = y 0 + v 0 t - g t 2 2

Em nosso caso teremos que

y t = v i t sin ⁡ θ - g t 2 sin ⁡ ϕ 2

Na qual

y m a x = v i v i sin ⁡ θ g sin ⁡ ϕ sin ⁡ θ - g 2 v i sin ⁡ θ g sin ⁡ ϕ 2 sin ⁡ ϕ

Na qual corta aqui, corta ali ... sobra apenas

y m a x = v i 2 sin 2 ⁡ θ g sin ⁡ ϕ - v i 2 sin 2 ⁡ θ 2 g sin ⁡ ϕ = v i 2 sin 2 ⁡ θ 2 g sin ⁡ ϕ

Passo 4

(d) Agora para determinarmos o deslocamento máximo na direção x , basta analisarmos que o máximo deslocamento ocorre quando y é nulo. Assim tome que

y t = v i t sin ⁡ θ - g t 2 sin ⁡ ϕ 2 = 0

v i sin ⁡ θ - g t sin ⁡ ϕ 2 = 0

Isolando t

t m a x = 2 v i sin ⁡ θ g s i n   ϕ

Assim temos o tempo na qual o movimento acontece. Tomando agora que a equação de movimento no eixo x é descrita por

x t = x 0 + v 0 t

Temos que para nosso problema

x t = v i t cos ⁡ θ

O que nos da que

x m a x = v i 2 v i sin ⁡ θ g s i n   ϕ cos ⁡ θ

x m a x = 2 v i 2 sin ⁡ θ cos ⁡ θ g sin ⁡ ϕ

Passo 5

(e) Se ϕ = 0 temos que o movimento ocorreria no plano horizontal. a = 0 , v → = v i cos ⁡ θ i → + v i sin ⁡ θ   j → , Δ y = 0 e Δ x = ∞

Se ϕ = 90 ° temos que o lançamento seria vertical. a = g ,   v → = v i cos ⁡ θ i → + v i sin ⁡ θ - g t j → ,   Δ y = v i 2 sin 2 ⁡ θ 2 g ,   Δ x = 2 v i 2 sin ⁡ θ cos ⁡ θ g

Resposta

  1. a → = - g sin ⁡ ϕ   j →
  2. v → = v i cos ⁡ θ i → + v i sin ⁡ θ - g t sin ⁡ ϕ j →
  3. Δ y = v i 2 sin 2 ⁡ θ 2 g sin ⁡ ϕ
  4. Δ x = 2 v i 2 sin ⁡ θ cos ⁡ θ g sin ⁡ ϕ

Exercícios de Livros Relacionados

O oásis A está 90k m a oeste do oásis B . Um camelo parte de A e leva 50h para caminhar 75k m na direção 37 ° ao norte do leste. Em seguida, leva 35h para caminhar 65k m para o sul e descansa por 5,0h
Na Fig. 4-49, uma estação de radar detecta um avião que se aproxima, vindo do Leste. Quando é observado pela primeira vez, o avião está a uma distância d 1 = 360m da estação e θ 1 = 40 ° acima do hori
Mostre que uma pedra atirada para cima leva o mesmo tempo na subida e na descida.
O vetor posição de um próton é inicialmente r →=5,0 i →- 6,0 j →+ 2,0 k → e depois se torna r → =- 2,0 i →+6,0 j →+ 2,0 k → , com todos os valores em metros. (a) Qual é o vetor deslocamento do próton?
Na cobrança do pênalti, no jogo de futebol, a bola é chutada à distância de 11m do gol, e a velocidade típica da bola é 100k m / h . O tempo que o goleiro gasta pra cair é aproximadamente igual ao tem