O átomo de hélio parcialmente ionizado é obtido quando apenas um dos dois elétrons é retirado.
Obs: realize todos os cálculos, incluindo frações.
Complete o diagrama abaixo dos níveis de energia para o , até e desenhe no diagrama as setas indicando as possíveis transições, onde ocorre a emissão de fótons, entre os estados.
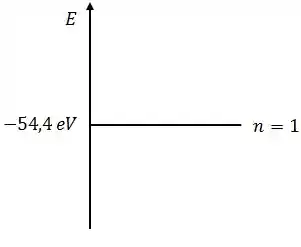
Calcule a energia do fóton emitido quando o elétron passa do estado de energia para o estado de energia .
Havendo uma mistura de e , é possível que o fóton do item emitido seja absorvido por algum átomo de ? Justifique a sua resposta através de cálculos.
Passo 1
Complete o diagrama abaixo dos níveis de energia para o , até e desenhe no diagrama as setas indicando as possíveis transições, onde ocorre a emissão de fótons, entre os estados.
Os níveis de energia são dados por:
Onde e .
O nosso único trabalho agora é calcular os valores de , , porque, se olharmos direito, para , que já foi dado no gráfico.
Então partiu!
O diagrama vai ficar com essa cara:
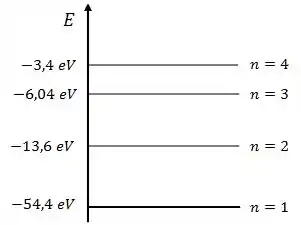
Passo 2
Para que haja emissão de fótons, é necessário que haja uma queda de energia. Essa energia “perdida” é transmitida para os fótons, fazendo com que haja emissão deles.
Assim, só haverá emissão de fótons na transição de um nível para outros níveis abaixo deste. Logo as transições ocorrerão da seguinte forma:
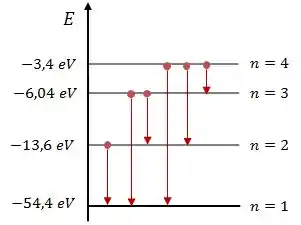
Adicionando as setas que indicam as possíveis transições, o diagrama vai ficar da seguinte forma:
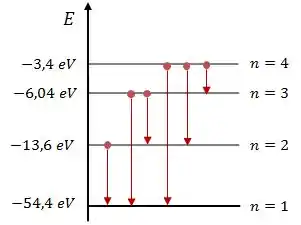
Passo 3
Calcule a energia do fóton emitido quando o elétron passa do estado de energia para o estado de energia .
A energia do fóton emitido será igual à diferença de energia entre os níveis 4 e 2. Isso acontece porque essa diferença de energia é transmitida para o fóton, fazendo com que haja a emissão dele.
Logo:
Passo 4
Havendo uma mistura de e , é possível que o fóton do item emitido seja absorvido por algum átomo de ? Justifique a sua resposta através de cálculos.
Para que o fóton emitido no item seja absorvido por algum átomo de é necessário que a diferença de energia entre quaisquer dois níveis de seja igual a .
Então vamos começar calculando as energias em cada nível.
Onde e, para , , logo:
Opa! Vamos calcular a diferença de energia entre os níveis 1 e 2.
Logo, o fóton pode ser absorvido pelo átomo de , que vai do nível 1 para o nível 2.
Resposta
Sim, o fóton pode ser absorvido pelo átomo de , que vai do nível 1 para o nível 2.