Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Complemento Ortogonal

Ver Teoria
Exercício 231234567891011121314151617181920212224252627

Enunciado

UFPE, 3°EE-2019.2

Considere o produto interno em P 3

a 0 + a 1 t + a 2 t 2 + a 3 t 3 ,   b 0 + b 1 t + b 2 t 2 + b 3 t ³ = 2 a 0 b 0 + a 1 b 1 + 2 a 2 b 2 + a 3 b 3

E seja W = [ 1 + t + t 2 ,   t - t 3 ] . Em relação a esse produto interno.

  1. Determine uma base ortogonal para W .
  2. Determine uma base para W ⊥ .

Passo 1

Belezera então pessoal, os pontos importantes que o enunciado trouxe pra gente é que o produto interno em P 3 está definido como:

a 0 + a 1 t + a 2 t 2 + a 3 t 3 ,   b 0 + b 1 t + b 2 t 2 + b 3 t ³ = 2 a 0 b 0 + a 1 b 1 + 2 a 2 b 2 + a 3 b 3

Onde a 0 + a 1 t + a 2 t 2 + a 3 t 3 e b 0 + b 1 t + b 2 t 2 + b 3 t ³ são dois polinômios quaisquer de P 3 .

E sabendo disso, ele deu pra gente o conjunto W = [ 1 + t + t 2 ,   t - t 3 ] . Na letra(a) ele tá pedindo pra gente determinar uma base ortogonal para W .

Mas calma aí chefe, porque temos um processo muito chique que faz exatamente isso de ortogonalizar um conjunto, ele chama; Processo de Ortogonalização de Gram-Schmidt. Que diz que dado um conjunto de vetores v = v 1 ,   v 2 , … ,   v n , os vetores do seu conjunto ortogonalizado w = w 1 ,   w 2 ,   … ,   w n são calculado como:

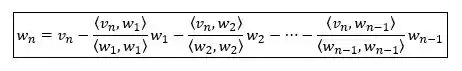
Passo 2

Sei que parece um pouquinho feio, mas vamos com carinho que vai dar certo, saca só. O primeiro passo do processo de Gram-Schmidt, é fixar o primeiro vetor/polinômio. Dado o conjunto W = [ 1 + t + t 2 ,   t - t 3 ] , o primeiro polinômio é o:

p 1 = 1 + t + t ²

Então:

w 1 = 1 + t + t 2

Show, então precisamos fazer com que o segundo vetor seja ortogonal a w 1 , então:

w 2 = p 2 - p 2 , w 1 w 1 , w 1 w 1

E substituindo os termos, temos:

w 2 =   t - t 3 -   t - t 3 , 1 + t + t 2 1 + t + t 2 , 1 + t + t 2 1 + t + t 2

Passo 3

E agora que vem a malandragem, porque o enunciado já deu pra gente como que calcula um produto interno entre dois vetores.

a 0 + a 1 t + a 2 t 2 + a 3 t 3 ,   b 0 + b 1 t + b 2 t 2 + b 3 t ³ = 2 a 0 b 0 + a 1 b 1 + 2 a 2 b 2 + a 3 b 3

Então para   t - t 3 , 1 + t + t 2 , temos que:

  t - t 3 = a 0 + a 1 t + a 2 t 2 + a 3 t 3 = 0 + 1 t + 0 t 2 + - 1 t 3

1 + t + t 2 = b 0 + b 1 t + b 2 t 2 + b 3 t 3 = 1 + 1 t + 1 t 2 + 0 t 3

Logo o produto interno fica assim:

a 0 + a 1 t + a 2 t 2 + a 3 t 3 ,   b 0 + b 1 t + b 2 t 2 + b 3 t ³ = 2 a 0 b 0 + a 1 b 1 + 2 a 2 b 2 + a 3 b 3

  t - t 3 , 1 + t + t 2 = 2 ( 0 ) ( 1 ) + 1 1 + 2 0 1 + - 1 0

  t - t 3 , 1 + t + t 2 = 0 + 1 + 0 + 0 = 1

Agora para 1 + t + t 2 , 1 + t + t 2 , temos que:

1 + t + t 2 , 1 + t + t 2 = 2 1 1 + 1 1 + 2 1 1 + 0 0

1 + t + t 2 , 1 + t + t 2 = 2 + 1 + 2 + 0 = 5

Portanto, juntando tudo que encontramos temos que:

w 2 =   t - t 3 -   t - t 3 , 1 + t + t 2 1 + t + t 2 , 1 + t + t 2 1 + t + t 2

w 2 =   t - t 3 - 1 5 1 + t + t 2

w 2 = t - t 3 - 1 5 - 1 5 t - 1 5 t 2

w 2 = - 1 5 + 4 5 t - 1 5 t 2 - t ³

E dessa forma, uma base β ortogonal para o conjunto W , é dada por:

β = w 1 ,   w 2

β = 1 + t + t 2 ,   - 1 5 + 4 5 t - 1 5 t 2 - t 3

Passo 4

Agora na letra (b), queremos encontrar uma base para W ⊥ .

Mas vamos devagarinho aqui também, primeiro vamos encontrar o complemento ortogonal de W , W ⊥ . Pra fazer isso, temos que levar em consideração que dado um polinômio p i de W ⊥ e um vetor w i de W vamos ter:

p i , w i = 0

Isso se deve pelo fato dos vetores serem ortogonais. Portanto, como temos apenas dois vetores em W , os vetores de W ⊥ precisarão respeitar as seguintes condições:

W ⊥ = a 0 + a 1 t + a 2 t 2 + a 3 t 3 : a 0 + a 1 t + a 2 t 2 + a 3 t 3 , 1 + t + t 2 = 0 a 0 + a 1 t + a 2 t 2 + a 3 t 3 ,   t - t 3 = 0

E aplicando as regras do produto interno definido pelo enunciado, temos que:

W ⊥ = a 0 + a 1 t + a 2 t 2 + a 3 t 3 : 2 a 0 + a 1 + 2 a 2 = 0 a 1 - a 3 = 0

Logo:

a 3 = a 1

E:

a 2 = 1 2 - 2 a 0 - a 1

a 2 = - a 0 - 1 2 a 1

Então quer dizer que nossos coeficientes de W ⊥ são:

a 0 ,   a 1 ,   a 2 ,   a 3 ⇔ a 0 ,   a 1 ,   - a 0 - 1 2 a 1 ,   a 1

Logo, o polinômio do tipo a 0 + a 1 t + a 2 t 2 + a 3 t 3 , fica assim:

W ⊥ = a 0 + a 1 t + - a 0 - 1 2 a 1 t 2 + a 1 t 3

W ⊥ = a 0 1 - t 2 ,   a 1 t - 1 2 t 2 + t 3

E dessa forma uma base β ' para o espaço W ⊥ é dada por:

β ' = 1 - t 2 , t - 1 2 t 2 + t 3  

Resposta

  1. β = 1 + t + t 2 ,   - 1 5 + 4 5 t - 1 5 t 2 - t 3
  2. β ' = 1 - t 2 , t - 1 2 t 2 + t 3  

Exercícios de Livros Relacionados

21. Seja { w 1 , w 2 , … ,w k } uma base de algum subespaço W de V . Mostre que W ⊥ consiste em todos os vetores de V que são ortogonais a cada um dos vetores da base.
20. Seja { v 1 ,v 2 ,… , v r } uma base de um espaço com produto interno V . Mostre que o vetor nulo é o único vetor em V que é ortogonal a cada um dos vetores da base.
Seja A x = 0 um sistema de m equações e n incógnitas. Mostre que x = x 1 x 2 ⋮ x n É uma solução do sistema se, e só se, o vetor x =( x 1 , x 2 , … , x n ) é ortogonal a cada vetor linha de A em relaç
18. Seja V um espaço com produto interno. Mostre que se w for ortogonal a ambos u 1 e u 2 , então w é ortogonal a k 1 u 1 + k 2 u 2 , quaiquer que sejam os escalares k 1 e k 2 . Interprete esse result
19. Seja V um espaço com produto interno. Mostre que se w for ortogonal a cada um dos vetores u 1 , u 2 , ... , u f , então w é ortogonal a cada vetor em ger{ u 1 , u 2 , ... , u f }.