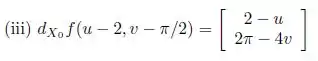Passo 1
A diferencial de uma função é dada por
Ou seja, o somatório dos produtos das derivadas parciais da função em relação as suas variáveis com seus respectivos valores de .
Passo 2
Vamos então calcular a matriz de derivadas dessa função:
Assim,
Em :
Passo 3
Agora falta só calcularmos o nosso , que nada mais é que a variação no vetor quando saímos de e vamos para , assim
Passo 4
Substituindo tudo na fórmula da diferencial:
Resposta
Exercícios de Livros Relacionados
Encontre r t se r ' t = 2 ti + 3 t 2 j + tk e r 1 = i + j .
Demonstre a fórmula 1 do Teorema 3.(d)/(d t) [u (t) + v (t)] = u^' (t) + v ' ( t )
Demonstre a fórmula 3 do Teorema 3. d d t f ( t ) u t = f ' t u t + f t u ' ( t )
Calcule a integral. ∫ 0 π / 2 3s e n 2 t cos ti + 3s e nt cos 2 t j + 2s e nt cos tk d t
Calcule a integral. ∫ 0 1 4 1 + t 2 j + 2 t 1 + t 2k d t