Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Derivadas - Matriz Jacobiana

Ver Teoria
Exercício 16123456789101112131415171819202122232425262728

Enunciado

UFF, Sem Campus, Cálculo IIB, P2 - Prof. Jorge Delgado - 2023 - Verão, Questão 5c

A função F r ,   θ ,   z = r   c o s   θ ,   r   s e n   θ , z fornece a mudança de variáveis para coordenadas cilíndricas de eixo z . As coordenadas ( r ,   θ ,   z ) são determinadas a partir do fato de que cada ponto x ,   y ,   z ∈ R 3 pertence ao cilindro de eixo z e raio igual a r = x 2 + y 2 = distância do ponto x ,   y ,   z até o eixo z , sendo θ o ângulo que o segmento da origem até x ,   y ,   0 faz com o semieixo positivo x no plano x y .

  1. Calcule o Jacobiano de F - 1 no ponto 2,0 , 1 .

Passo 1

Eaee!!! Belezinha? Bom... a questão nos pede para calcularmos o Jacobiano de F - 1 no ponto 2,0 , 1 .

Mas o que é esse Jacobiano?

Bom... a matriz Jacobiana é a matriz formada pelas derivadas parciais de primeira ordem de uma função vetorial. Veja:

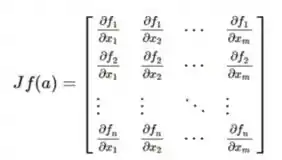
E o Jacobiano nada mais é do que o determinante da matriz Jacobiana!!

Agora vamos aplicar!!

Passo 2

Bom... Para determinar a matriz Jacobiana de F r ,   θ ,   z , faz-se:

D F r ,   θ ,   z = ∂ F 1 ∂ r ∂ F 1 ∂ θ ∂ F 1 ∂ z ∂ F 2 ∂ r ∂ F 2 ∂ θ ∂ F 2 ∂ z ∂ F 3 ∂ r ∂ F 3 ∂ θ ∂ F 3 ∂ z ∴

Onde F 1 = r cos ⁡ θ ,   F 2 = r   s e n θ e F 3 = z .

Dessa forma, fazendo as derivadas parciais, temos:

D F r ,   θ ,   z = cos ⁡ θ -   r   s e n   θ 0 s e n   θ r cos ⁡ θ 0 0 0 1

Passo 3

Agora, fazendo o Jacobiano, basta fazermos o determinante da matriz que encontramos agora pouco:

J F r ,   θ ,   z = cos ⁡ θ -   r   s e n   θ 0 s e n   θ r cos ⁡ θ 0 0 0 1 ∴

J F r ,   θ ,   z = r cos 2 ⁡ θ + r   s e n 2   θ ∴

J F r ,   θ ,   z = r

Passo 4

Assim, para o ponto 2,0 , 1 , temos:

F 2,0 , 1 = 2 cos ⁡ 0 ,   2   s e n   0 ,   1 = 2,0 , 1

Dessa forma, F - 1 é dada da seguinte forma:

J F - 1 2,0 , 1 = J F - 1 F 2,0 , 1 ∴

J F - 1 2,0 , 1 = 1 J F 2,0 , 1 ∴

J F - 1 2,0 , 1 = 1 r ∴

J F - 1 2,0 , 1 = 1 2

Entendeu direitinho? Responde aee ;)

Resposta

J F - 1 2,0 , 1 = 1 2

Exercícios de Livros Relacionados

Encontre r t se r ' t = 2 ti + 3 t 2 j + tk e r 1 = i + j .
Demonstre a fórmula 1 do Teorema 3.(d)/(d t) [u (t) + v (t)] = u^' (t) + v ' ( t )
Demonstre a fórmula 3 do Teorema 3. d d t f ( t ) u t = f ' t u t + f t u ' ( t )
Calcule a integral. ∫ 0 π / 2 3s e n 2 t cos ⁡ ti + 3s e nt cos 2 ⁡ t j + 2s e nt cos ⁡ tk d t
Calcule a integral. ∫ 0 1 4 1 + t 2 j + 2 t 1 + t 2k d t