(b)Em um outro experimento, as duas fendas do item (a) são substituídas por uma única fenda de largura a = 2 . m. Determine, em metros, a largura do máximo central da figura de difração observada no anteparo. Sugestão: substitua os valores numéricos apenas na resposta final.
Passo 1
Vamos entender visualmente o que o enunciado está falando
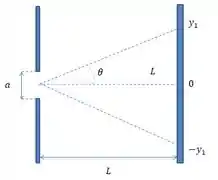
Agora no item b substituiremos as nossas duas fendas por uma única fenda de largura a como mostra a figura acima. Tome cuidado pois agora essa fenda não pode mais ser considerada como uma fenda pontual, logo as suas fórmulas e comportamentos serão diferentes das usuais para o caso das fendas pontuais.
Mas o que o exercício quer?
O exercício quer que definamos o tamanho, ou seja, largura do máximo central, mas para fendas simples, a fórmula que nos da os mínimos, e aqui vale uma observação, pois para fendas duplas a fórmula dava máximos, mas para fendas simples ela nós dará mínimos e a fórmula é a seguinte.
Em que m=
Agora pensa no seguinte, se conseguirmos definir a distancia entre dois mínimos em torno do centro, descobriremos exatamente o valor da largura do máximo central.
Passo 2
De novo podemos considerar que é muito pequeno, logo
E pelo desenho que fizemos podemos considerar pelo triangulo que
Substituindo isso na nossa equação para franjas simples, teremos que
E isolando o valor de encontraremos
Passo 3
Como queremos a largura do máximo central faremos a variação de distância entre os valores para m=1 e m=-1, que são os primeiros mínimos em torno do máximo central.
Para m=1 temos
Para m=-1 temos -
Logo a diferença será
Então teremos que
Os dados na nossa questão são
m=1
m
m
m
Substituindo
Então a largura do máximo central será
Resposta
b)