Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Difração em Fenda Simples

Ver Teoria
Exercício 3312345678910111213141516171819202122232425262728293031323435363738

Enunciado

Duas fendas separadas por 0,10   m m são iluminadas com luz verde ( λ   =   540   n m ). Calcule a distância (em cm) da região central brilhante até a quinta faixa brilhante se a tela estiver 1,0   m atrás das fendas.

  1. 2,3   c m
  2. 2,5   c m
  3. 2,7   c m
  4. 2,1   c m
  5. 2,0   c m

Passo 1

Bem, imagina aqui então que tenhamos fenda dupla separada por 0,10   m m e temos um anteparo como na figura a baixo...

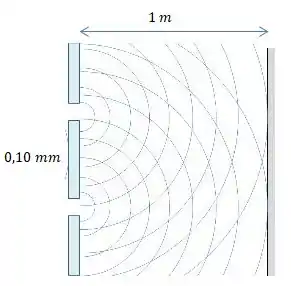
Pelas fendas duplas passa uma luz que forma no anteparo um padrão luminoso em faixas...

Nesse problema, nós queremos a distância da faixa central mais brilhante até a quinta faixa mais brilhante.

Passo 2

Bem, de acordo com a nossa teoria de fendas duplas, podemos calcular a distância ∆ y entre dois “máximos” (duas faixas claras) usando a equação...

∆ y = R ∆ m   λ d

Onde R é a distância da fenda ao anteparo ( R = 1,0   m ),   d é a separação entre uma fenda e outra ( d = 0,10   m m = 0,10 ⋅ 10 - 3   m ) e m é a posição da faixa.

Então veja bem, a faixa do meio (mais clara) tem m = 0 , a primeira faixa depois dela tem número 1 , a quinta faixa clara depois dela vai ter m = 5 ...

Então, no nosso caso estamos querendo a distância entre a faixa mais clara ( m = 0 ) para a 5ª faixa mais clara ( m = 5 ), ou seja...

∆ m = 5 - 0 = 5

Então...

∆ y = R ∆ m   λ d   →

∆ y = 1 5 540   n m 0,10 ⋅ 10 - 3

Não se esqueça de que nano é o mesmo que 10 - 9 ...

∆ y = 5 540 ⋅ 10 - 9   0,10 ⋅ 10 - 3   →

∆ y = 5 540 ⋅ 10 - 9   10 - 4   →

∆ y = 27 00 ⋅ 10 - 5   →

Esse resultado está em m e t r o s para passar para centímetro, basta sobrar 10 - 2 ali, então a gente meche na vírgula até isso acontecer...

∆ y = 2,7 00 ⋅ 10 - 2   →

Prontinho, isso significa que a distância até a quinta amarela é...

∆ y = 2,7   c m

Resposta

Letra C

Exercícios de Livros Relacionados

19. A estação de rádio pública K X P R - F M de Sacramento transmite a 88,9M H z . As ondas de rádio passam entre dois arranha-céus. A distância entre as paredes mais próximas dos dois arranha-céus é
Um padrao de difracao de fenda simpleseformado usando luz de laser monocromatico com comprimento de onda de 450 nm. Oque acontece com a distancia entre o primeiro maximo e o maximo central quando a la
Quando uma rede de difracaoeiluminada com luz branca,o maximo de primeira ordem da luz verde(a)esta mais proximo do maximo central que o maximo de primeira ordem da luz vermelha,(b)esta mais proximo d
A medida da distância até a Lua (distância lunar) é rotineiramente feita através de pulsos curtos de laser e da medida do tempo que eles levam para refletir na Lua. Um pulso é disparado da Terra. Para
Microondas planas incidem em uma fina placa metálica que tem uma fenda longa e estreita de largura 5c m . Radiação de microondas incide na lâmina com incidência normal. O primeiro mínimo de difração é