Em um experimento de difração por uma fenda simples, ao se aumentar a largura da fenda, pode-se afirmar que
a) a largura da faixa brilhante diminui.
b) as distâncias entre faixas escuras consecutivas aumentam.
c) o comprimento de onda da radiação que passa pela fenda aumenta.
d) a intensidade da radiação que passa pela abertura diminui.
Passo 1
Eai galerinha, bora resolver mais um problema de física 4 da UFRJ?
Nesse problema vamos discutir difração por uma fenda simples de largura . Sabemos que para uma fenda, a expressão da intensidade é dada por
Com isso, os mínimos ocorrem quando
Logo, os mínimos ocorrem para
Cuidado que para temos uma indeterminação na expressão para a intensidade de modo que esse ponto não corresponde a um mínimo, na verdade ele corresponde a um máximo! O desenho que ilustra a situação é mostrado a seguir:
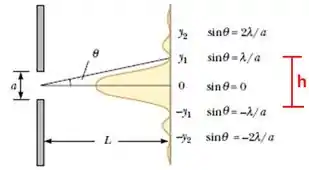
Para achar a largura da franja central, usamos que
Como os ângulos são pequenos, podemos usar a aproximação:
Desta forma,
Isolando a largura da franja central, achamos
Passo 2
Vemos da última expressão que aumentando a largura da fenda , a largura da franja central deve diminuir, pois elas são inversamente proporcionais! Com isso, a alternativa A está correta!
Além disso, vemos que aumentando o tamanho da fenda , a distância entre os pontos de mínimo diminui, o que é contrário do que é dito na afirmativa B. Logo ela está errada!
As afirmativas C e D também estão erradas! Com isso, devemos assinalar a alternativa A 😊.
Resposta
Alternativa A.