Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Difração em Fenda Simples

Ver Teoria
Exercício 1012345678911121314151617181920212223242526272829303132333435363738

Enunciado

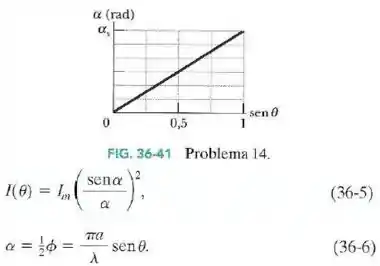
A Fig.36-41 mostra a variação do parâmetro α da Eq.36-6 com o seno do ângulo θ em um experimento de difração de fenda única usando uma luz com um comprimento de onda de 610 n m .

A escala do eixo vertical é definida por α s = 12   r a d . Determine:

  1. A largura da fenda.
  2. O número total de mínimos de difração (dos dois lados do máximo central).
  3. O menor ângulo para o qual existe um mínimo.
  4. O maior ângulo para o qual existe um mínimo.

Passo 1

a)

Sabemos que

α = π a λ sen ⁡ ( θ )

Para sen ⁡ ( θ ) = 1 , temos α = α s = 12   r a d . Além disso, o comprimento de onda da luz é de λ = 610   n m = 610 ∙ 10 - 9   m .

Rearranjando a equação:

a = α s λ π = 12 ∙ 610 ∙ 10 - 9 π ≅ 2   330 ,   03 ∙ 10 - 9   m ≅ 2,33   μ m

Passo 2

b)

A condição do mínimo de difração é:

sen ⁡ ( θ ) = m λ a

O mínimo de difração com maior ângulo possível tem que ter um ângulo menor que 90 ° . Para acharmos esse mínimo, vemos qual seria o valor de m para este ângulo.

m = sen ⁡ θ ∙ a λ ≅ sen ⁡ 90 ° ∙ 2,33 ∙ 10 - 6 610 ∙ 10 - 9 ≅ 3,82

O último mínimo a aparecer no anteparo será o de ordem m = 3 . Assim, temos 3 mínimos até chegar nesse.

Porém, temos que contar também os mínimos que aparecem abaixo do máximo central (ângulos negativos), que serão mais 3 mínimos, pois a figura é simétrica.

Temos no total 6 mínimos de difração.

Passo 3

c)

O menor ângulo para o qual temos um mínimo é aquele correspondente ao primeiro mínimo m = 1 .

sen ⁡ ( θ ) = λ a = 610 ∙ 10 - 9 2,33 ∙ 10 - 6 ≅ 0,262

θ = sen - 1 ⁡ ( 0,262 ) ≅ 0,265   r a d ≅ 15,18 °

Passo 4

d)

O maior ângulo para o qual existe um mínimo é aquele corresponde ao último mínimo do anteparo, que é o mínimo de ordem 3 .

sen ⁡ ( θ ) = 3 ∙ λ a = 3 ∙ 610 ∙ 10 - 9 2,33 ∙ 10 - 6 ≅ 0,785

θ = sen - 1 ⁡ ( 0,785 ) ≅ 0,903   r a d ≅ 51,76 °

Resposta

a)

a ≅ 2,33   μ m

b)

No total teremos 6 mínimos de difração.

c)

θ ≅ 0,265   r a d ≅ 15,18 °

d)

θ ≅ 0,903   r a d ≅ 51,76 °

Exercícios de Livros Relacionados

19. A estação de rádio pública K X P R - F M de Sacramento transmite a 88,9M H z . As ondas de rádio passam entre dois arranha-céus. A distância entre as paredes mais próximas dos dois arranha-céus é
Um padrao de difracao de fenda simpleseformado usando luz de laser monocromatico com comprimento de onda de 450 nm. Oque acontece com a distancia entre o primeiro maximo e o maximo central quando a la
Quando uma rede de difracaoeiluminada com luz branca,o maximo de primeira ordem da luz verde(a)esta mais proximo do maximo central que o maximo de primeira ordem da luz vermelha,(b)esta mais proximo d
A medida da distância até a Lua (distância lunar) é rotineiramente feita através de pulsos curtos de laser e da medida do tempo que eles levam para refletir na Lua. Um pulso é disparado da Terra. Para
Microondas planas incidem em uma fina placa metálica que tem uma fenda longa e estreita de largura 5c m . Radiação de microondas incide na lâmina com incidência normal. O primeiro mínimo de difração é