Uma radiação eletromagnética, de comprimento de onda se propagando no ar, incide perpendicularmente sobre um plano contendo uma única fenda, cuja largura é .
Uma figura de difração é observada sobre um anteparo situado à uma distância do plano da fenda. Determine:
- a posição angular dos mínimos de difração observados no anteparo no intervalo ;
- o número de máximos observados no intervalo ;
- a diferença espacial entre os mínimos de difração de ordem e ;
Passo 1
Letra a)
Na difração por fenda simples, os mínimos são observados nos ângulos correspondentes à condição:
Onde é a largura da fenda e é o comprimento de onda da luz. Vamos então calcular cada um dos mínimos pela fórmula:
Agora substituindo os valores de :
Que são a posição angular dos mínimos em questão.
Passo 2
Letra b)
Entre dois mínimos se encontra sempre um máximo (não necessariamente no meio dos dois mínimos).
Assim, eu tenho além do máximo central, três máximos de um lado () que estão entre os quatro mínimos e três do outro (), o que corresponde a um total de sete máximos.
Passo 3
Letra c)
Neste caso, os ângulos envolvidos são muito grandes, e não poderíamos usar a aproximação de pequenos ângulos. Porém, se a prova der alguma indicação de que pode (como por exemplo, não deixar usar calculadora), então vai fundo e sem medo.
Por via das dúvidas, vou resolver das duas formas aqui pra te mostrar como faz.
Sem a aproximação, temos que usar a tangente dos ângulos para achar a posição de cada mínimo no anteparo.
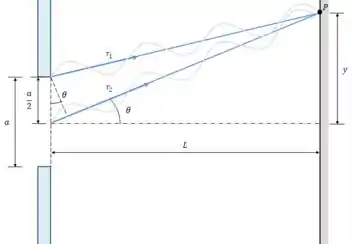
De acordo com o enunciado, a distância da fenda até o anteparo é . Para o mínimo correspondente a , temos:
Para , temos:
A distância entre eles fica:
Agora, qual seria essa distância se usássemos nossa aproximação mágica?
Neste caso, teríamos:
E assim:
Podemos deixar e em nanômetros, pois a unidade de um irá cortar com a do outro, e teremos no fim o na mesma unidade de .
A distância entre os dois seria:
O que nos deixa claro que essa aproximação não é nem um pouco razoável.
Resposta
Letra a)
Letra b)
Letra c)