Uma onda plana monocromática incide em uma fenda retangular de largura . A direção de propagação da onda incidente é perpendicular ao plano da abertura. Um padrão de difração é observado em um anteparo bem distante da abertura.

Imagine que, para um ponto do anteparo, a diferença do caminho percorrido entre a onda secundária produzida pelo ponto mais alto da abertura e a onda secundária produzida pelo ponto médio seja um comprimento de onda da luz incidente.

Pode-se afirmar que este ponto corresponde ao:

1. Primeiro mínimo de difração
2. Segundo mínimo de difração
3. Primeiro máximo de difração
4. Segundo máximo de difração
5. Terceiro mínimo de difração
6. Terceiro máximo de difração

WARNING! WARNING!

Essa pergunta é uma pegadinha! Cuidado!

Ela tenta usar a forma de deduzir a posição dos mínimos de difração que se usa pra ver a equação de forma mais “simples”, onde dividimos a fenda em , em , em e por aí vai, usando diferenças de fase de para duas partes consecutivas dessa divisão.

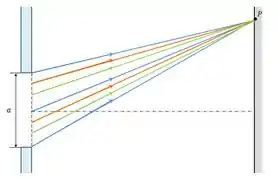
Neste caso em específico, o topo e o meio da fenda ter uma diferença de fase de NÃO SIGNIFICA MÁXIMO DE DIFRAÇÃO!

O motivo é que, se pegarmos o ponto exatamente entre esses dois, a diferença entre ele e o topo será de (porque dividimos a diferença de caminho por ) e teremos interferência destrutiva.

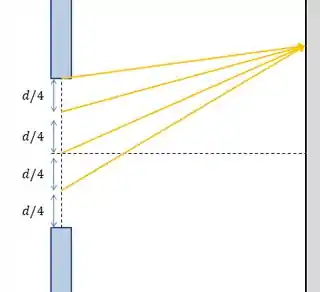
O ponto do meio também vai sofrer interferência destrutiva, mas com o ponto abaixo dele, a uma distância de . Se formos descendo uma distância dos dois pontos, teremos novos pontos que também se cancelam (porque também se distanciam um do outro).

Isso significa então que esse é um ponto de mínimo.

Mas qual mínimo ele vai ser? A resposta é: o segundo.

De fato:

O motivo é que o primeiro é dado por uma construção parecida, mas onde a diferença de fase entre o ponto de cima e o ponto do meio já é , o que daria:

Assim, nossa resposta é a letra , segundo mínimo de difração.