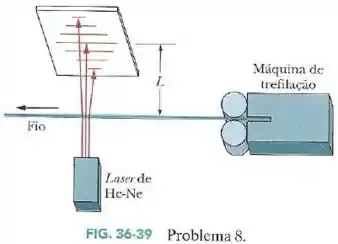
Os fabricantes de fios (e outros objetos de pequenas dimensões) às vezes usam um laser para monitorar continuamente a espessura do produto. O fio intercepta a luz do laser, produzindo uma figura de difração parecida com a de uma fenda com a mesma largura que o diâmetro do fio (Fig.36-39).
Suponha que o fio é iluminado com um laser de hélio-neônio, com um comprimento de onda de , e que a figura de difração aparece em uma tela situada a uma distância do fio. Se o diâmetro do fio é , qual é a distância observada entre dois mínimos de décima ordem (um de cada lado do máximo central) ?
Passo 1
Neste exercício, nós queremos saber a distância entre dois mínimos de décima ordem, um de cada lado do máximo central.
Quanto maior a ordem de um dado mínimo, maior a distância angular dele até o centro da figura. Por isso, já que estamos trabalhando com o mínimo de décima ordem, é mais seguro nós não considerarmos válida a aproximação de pequenos ângulos e tentarmos resolver o exercício da forma mais exata possível.
Passo 2
Primeiramente nós encontramos a distância angular dos mínimos até o centro da figura. Isso pode ser feito pelas condições de interferência totalmente destrutiva:
O comprimento de onda da luz é de , o tamanho da “fenda” (diâmetro do fio) é e os mínimos são de ordem .
Neste caso, mesmo trabalhando com um mínimo de ordem alta, nós vemos que poderíamos ter usado a aproximação de pequenos ângulos desde o início.
Passo 3
Tendo confirmado que podemos usar a aproximação de pequenos ângulos, daqui podemos seguir o caminho que quisermos:
- Usar os dois ângulos calculados para encontrar a distância entre eles a partir da tangente ;
- Usar direto a fórmula aproximada para a distância entre dois mínimos .
Por comodidade, usarei a segunda que já nos dá direto o valor procurado, sendo a distância do fio até o anteparo de .
Apenas por desencargo de consciência, vamos calcular da forma mais exata e comprovar que ambos os caminhos dariam aproximadamente o mesmo resultado.
Substituindo os ângulos:
Ou seja, neste caso, ambos os caminhos são igualmente válidos.
Resposta
A distância observada entre os dois mínimos de décima ordem é .