UFU, Sem Campus, Cálculo 1 - Listas de Cálculo 1, Questão 4.6
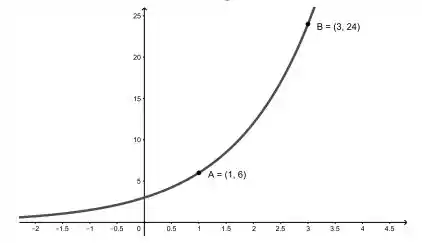
Encontre a função exponencial cujo gráfico é dado abaixo. Em seguida, determine o gráfico da sua inversa, bem como sua lei de formação.
Passo 1
Eaew, tudo certinho contigo?
Temos que encontrar as constantes e da função exponencial
Além disso, temos que encontrar a inversa dessa função e esboçar o seu gráfico.
Vem comigo!
Passo 2
Primeiro vamos encontrar as constantes, para isso observamos que a questão nos informou dois pontos associados a função
e
Então, para o ponto , temos
para o ponto , temos
Passo 3
Substituindo na equação do primeiro ponto
Assim,
Então,
Encontrando
Passo 4
Então a função exponencial é
Passo 5
Agora vamos encontrar a inversa, isolando
Então
Trocando e , temos a inversa
Note que
e
Passo 6
Esboçando o gráfico da inversa
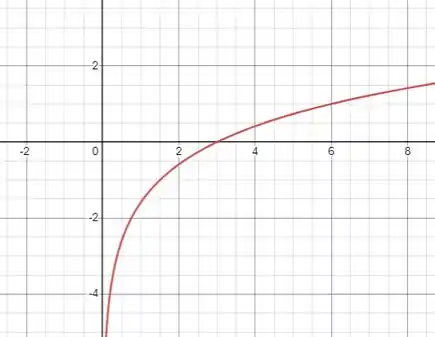
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
No decorrer da resolução.