UFSC – Pré Cálculo – Exame – Questão 18
Qual é o domínio da função
É igual a:
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui!
O problema pediu para acharmos o domínio de uma função inversa trigonométrica, aqui ó
Sabemos que o seno tem imagem entre certo? Mas o que tem isso a ver com a função arco seno?
Mas calma! A ideia aqui é encontrar os intervalos que cada uma das desigualdades é satisfeita (de cada lado) e no fim comparar os resultados: no intervalo onde essas duas condições são satisfeitas simultaneamente será nossa resposta!!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Primeiro vamos ver a inequação da esquerda:
Reorganizando temos o seguinte
Temos que encontrar onde essa equação de segundo grau é negativo ou zero. Então vamos achar as raízes e avaliar o sinal em torno desses pontos
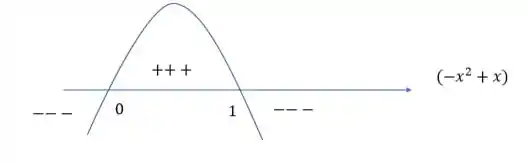
Queremos o intervalo onde essa função é , então é antes de e depois de (incluindo os pontos):
Beleza?
Passo 3
Agora vamos olhar a inequação do lado direito e repetir o raciocínio!
Reorganizando temos
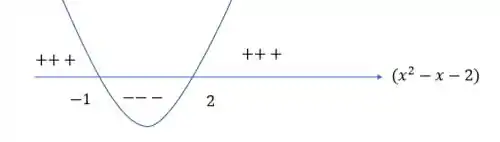Aí fazendo um pequeno esboço temos
Nosso intervalo de interesse é onde a função é , então:
Tudo bem até aqui? Agora precisamos juntar esses intervalos!
Passo 4
Vamos fazer uma comparação dos intervalos e ver em qual pedaço (ou pedaços) em que as DUAS condições são satisfeitas!
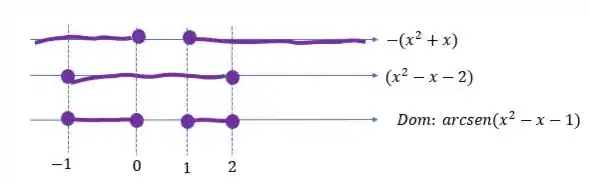
Embora o ponto não faça diferença para a condição do , quando comparamos os intervalos é importante colocar, assim podemos ver que o está contido nos dois intervalos, tanto quanto o e entre eles. Mas antes do só funciona para a primeira condição, então esse pedaço não entra na solução final!
A mesma coisa acontece com o pedaço entre 0 e 1, e depois de 2. Eles são válidos apenas para alguma condição, e não para as duas! Por isso no fim, nossa solução fica assim
E a alternativa correta é (B)
E é isso!
Espero ter ajudado! Vamos para a próxima?