17. Seja . O valor de é:
- Nenhuma das outras respostas.
Passo 1
Oi, galerinha! Tudo bom? Nessa questão temos uma soma de cossenos para calcular. Mas, repara, que todos os ângulos são dados por , onde é um número inteiro impar.
Então para saber quanto vale cada cosseno vamos ter que olhar para círculo trigonométrico:
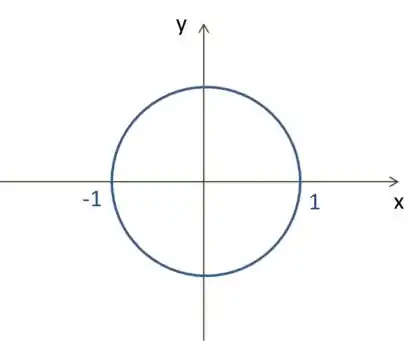
Agora precisamos saber qual volta foi dada em cada ângulo e identificar quanto vale o cosseno.
Bora lá!
Passo 2
Começando por
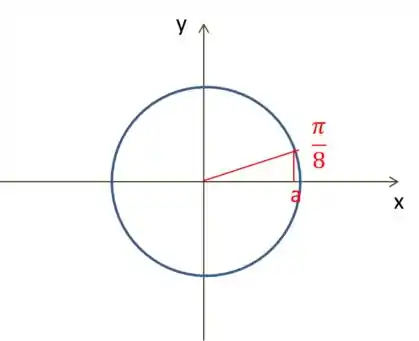
Note que arbitramos um valor para esse cosseno. Logo:
Passo 3
Para o ângulo , podemos dizer que ele andou . Dando essa volta no nosso círculo, ficamos com,

Repara que ficamos com o mesmo ângulo em relação a só que negativo. Logo:
Passo 4
Para o ângulo , podemos dizer que ele andou . Dando essa volta no nosso círculo, ficamos com,
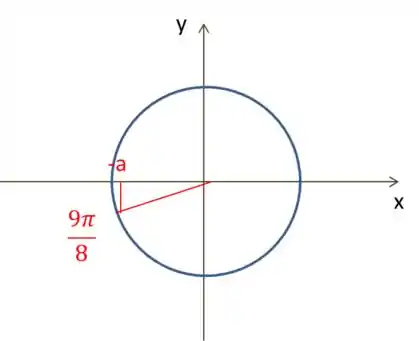
Repara que ficamos com o mesmo ângulo em relação a só que negativo e no terceiro quadrante. Logo:
Passo 5
Por fim, o ângulo , podemos dizer que ele andou . Dando essa volta no nosso círculo, ficamos com,
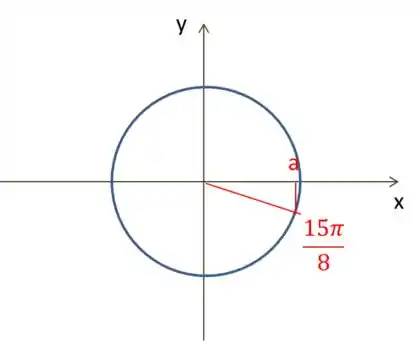
Repara que retornamos para positivo, só que no quarto quadrante. Logo:
Passo 6
Somando tudo, ficamos com
Prontinho!