O período da função vale:
Passo 1
Falaaaaa Aí!! Como podemos encontrar o período dessa função???
Sabemos que o período da função cotangente é igual a , certo!?
Vamos partir daqui então!!
Passo 2
Para determinarmos o período, pegaremos o número que está acompanhando o
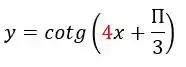
Que no nosso caso aqui será o número e faremos o seguinte
Agora, vamos isolar o para descobrir qual é o período da função . Assim,
Portanto, a nossa resposta é a letra C!!
Resposta
Letra C
Exercícios de Livros Relacionados
30. Em cada parte , esboce o gráfico e verifique seu trabalho com um recurso computacional. f x = 3 arcsin x 2 . f x = arccos x - π 2 . f x = 2 arctan - 3 x . f x = arccos x + arcsin x .
Prove que:
Utilize o resultado do exercício 59 para mostrar que:
Prove que:
29. Em cada parte encontre o valor numérico exato da expressão dada: cos arccos 4 5 + arcsin 5 13 . sin arcsin 4 5 + arccos 5 13.