Verifique a identidade
Passo 1
Vamos lááá!! Queremos verificar que a igualdade é valida, beleza?!
Vamos partir de
E mostrar que conseguimos chegar em
Beleza?!
Passo 2
Se você reparar, temos o produto de uma soma e uma diferença! Podemos então utilizar os Produtos Notáveis! Não lembra??? Eu lembro pra você! Utilizaremos aqui
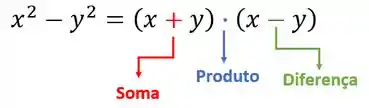
Assim,
Show de bola?!
Passo 3
EPAAAAAA! Se você reparar, temos uma identidade trigonométrica que diz que
Que é exatamente a expressão que encontramos após aplicar o Produto Notável!
Assim,
Beleza?!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
30. Em cada parte , esboce o gráfico e verifique seu trabalho com um recurso computacional. f x = 3 arcsin x 2 . f x = arccos x - π 2 . f x = 2 arctan - 3 x . f x = arccos x + arcsin x .
Prove que:
Utilize o resultado do exercício 59 para mostrar que:
Prove que:
29. Em cada parte encontre o valor numérico exato da expressão dada: cos arccos 4 5 + arcsin 5 13 . sin arcsin 4 5 + arccos 5 13.