Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Operações com Vetores

Ver Teoria
Exercício 1212345678910111314151617181920212223

Enunciado

USP – Álgebra Linear – P1 2021 – Questão 12

Considere, em E 3 , o triângulo de vértices A , B , C . Seja X o ponto sobre o lado B C tal que X C = 3 B X e seja Y o ponto no segmento A X tal que Y X = 2 A Y . Seja Z o ponto sobre o lado A B que está na reta que passa por C e Y , conforme a figura (fora de escala):

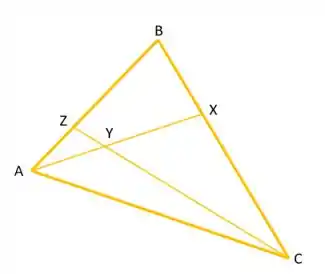
Se α ∈ R satisfaz A Z = α . A B , então α é igual a

a) 3 19

b) 4 19

c) 3 11

d) 1 7

e) 2 7

f) 2 11

Passo 1

E aíí galera, prontos pra essa questão mais geométrica?

Aqui nós vamos ter que brincar com os vetores para encontrarmos o valor de α , tal que A Z = α . A B . Ou seja, sabemos que A Z e A B são paralelos, mas em que escala?

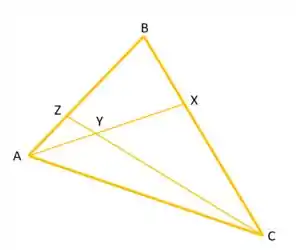
O nosso ponto de partida aqui vai ser que

α . A B = A Z

α . A B = A Y + Y Z

Vamossss lááá

Passo 2

Temos que

α A B = A Y + Y Z

α A B = A Y + Y Z

Sabemos que Y X = 2 A Y , então A Y = 1 3 A X

Como Y Z está na mesma reta que C Z , podemos escrever Y Z = β . C Z , onde β é um escalar

α A B = 1 3 A X + β . C Z

α A B = 1 3 A B + B X + β . C A + A Z

Como X C = 3 B X , então B X = 1 4 B C

α A B = 1 3 A B + 1 4 B C + β . C A + A Z

α A B = 1 3 A B + 1 3 . 1 4 B C + β . C A + β . A Z

α A B = 1 3 A B + 1 12 B A + A C + β . C A + β . A Z

Passo 3

Sabemos que A Z = α . A B

α A B = 1 3 A B + 1 12 B A + A C + β . C A + β . α . A B

α A B = 1 3 A B + 1 12 - A B + A C - β . A C + β . α . A B

α A B = 1 3 A B - 1 12 A B + 1 12 A C - β . A C + β . α . A B

Colocando os termos comuns em evidência

α A B + 0 . A C = A B . 1 3 - 1 12 + β . α + A C . 1 12 - β

Passo 4

Temos que

α A B + 0 . A C = A B . 1 3 - 1 12 + β . α + A C . 1 12 - β

Como A B e A C são LI, podemos igualar os coeficientes que estão multiplicando os mesmos termos:

1 3 - 1 12 + β . α = α 1 12 - β = 0

Da segunda equação, temos que β = 1 12 . Substituindo na primeira:

1 3 - 1 12 + 1 12 α = α

4 12 - 1 12 = 12 α 12 - 1 α 12

11 α 12 = 3 12

Então:

11 α = 3

α = 3 11

A alternativa correta é a letra C, fechou?

Resposta

c) α = 3 11

Exercícios de Livros Relacionados

Determine uma equação da esfera com centro em ( 2 , - 6 , 4 ) e raio 5 . Descreva sua intersecção com cada um dos planos coordenados.
Diz-se que o vetor v é combinação linear dos vetores v 1 ,v 2 ,...,v n quando se tem v=α 1 v 1+α 2 v 2+···+α n v n ,c o mα 1 ,α 2 ,...,α n∈R . Mostre que os vetores u ,vew são coplanares se, e somente
Determine uma equação da esfera com centro em ( 0 , 1 , - 1 ) e raio 4 . Qual é a intersecção dessa esfera com o plano y z ?
Escreva inequações para descrever a região dada.34. O cilindro sólido que está sobre ou abaixo do plano z = 8 e sobre ou acima do disco no plano x y com centro na origem e raio 2 .
Determine uma equação para o conjunto de pontos equidistantes dos pontos A ( - 1,5 , 3 ) e B ( 6,2 , - 2 ) . Descreva o conjunto.