P1 de Álgebra Linear da UFRJ - 2018.1

Considere o problema de se encontrar dois números cuja soma seja igual a a, cuja diferença seja igual a b e tais que o triplo do primeiro mais o quíntuplo do segundo seja igual a c.

(a) Quando este problema tem solução, ela é única.

(b) Este problema nunca tem solução.

(c) Este problema sempre tem solução.

(d) Quando este problema tem solução, ela não é única.

Sejam , e A tal que e . Calcule a terceira coluna da matriz A.

(a)

(b)

(c)

(d)

(I) Um sistema linear com mais equações do que incógnitas pode ter solução única.

(II) Um sistema linear com menos equações do que incógnitas pode ter solução única.

(a) I é verdadeira e II é falsa

(b) I é falsa e II é verdadeira

(c) Ambas são verdadeiras

(d) Ambas são falsas

Assinale a solução geral do sistema

(a)

(b)

(c)

(d)

Considere a matriz

(a) e

(b) e

(c) e

(d) e

Se é solução do sistema

então x + z é igual a:

(a) 11

(b) 9

(c) 5

(d) 7

é base do se:

(a)

(b)

(c)

(d)

Se então, necessariamente:

(I) O conjunto é linearmente dependente.

(II) não pertence ao conjunto gerado por e .

(a) I é verdadeira e II é verdadeira.

(b) I é falsa e II é verdadeira.

(c) I é falsa e II é falsa.

(d) I é verdadeira e II é falsa.

Sejam uma base de G e .

(I) O vetor necessariamente pertence a um dos planos ou

(II) Se e são LI, então é LD.

(a) I é verdadeira e II é verdadeira.

(b) I é falsa e II é falsa.

(c) I é verdadeira e II é falsa.

(d) I é falsa e II é verdadeira.

Cada representa um número diferente de 0. (Diferentes ’s podem assumir valores distintos!). O sistema que pode não ter solução é:

É uma base do núcleo de:

(a)

(b)

(c)

(d)

Determine a dimensão do conjunto abaixo

(a) 1

(b) 2

(c) 3

(d) 4

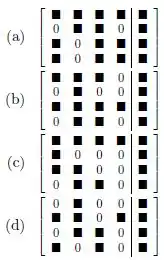
Assinale a matriz cuja imagem é um plano e cujo núcleo é uma reta.

(a)

(b)

(c)

(d)

Dada uma matriz A, seja L uma matriz obtida reordenando-se as linhas de A e seja C uma matriz obtida reordenando-se as colunas de A.

(I) Se tem solução, então também tem solução.

(II) Se tem solução única, então também tem solução única.

(a) I é falsa e II é falsa.

(b) I é verdadeira e II é falsa.

(c) I é falsa e II é verdadeira.

(d) I é verdadeira e II é verdadeira.

Qual dos sistemas abaixo possui um conjunto-solução de dimensão 2?

(a)

(b)

(c)

(d)

Seja um conjunto linearmente independente e uma combinação linear de e .

(I) e não podem ser ambos linearmente independentes.

(II) e podem ser ambos linearmente dependentes.

(a) I é verdadeira e II é falsa

(b) Ambas são verdadeiras

(c) I é falsa e II é verdadeira

(d) Ambas são falsas

Considere os seguintes sistemas lineares:

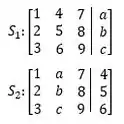
(I) Existem valores de a, b e c tais que o sistema não tem solução.

(II) Existem valores de a, b e c tais que o sistema não tem solução.

(a) I é verdadeira e II é falsa

(b) I é falsa e II é verdadeira

(c) Ambas são verdadeiras

(d) Ambas são falsas