Cada representa um número diferente de 0. (Diferentes ’s podem assumir valores distintos!). O sistema que pode não ter solução é:
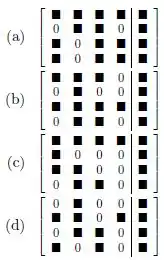
Passo 1
Todas as alternativas mostram sistemas com 4 equações e 4 incógnitas. Vamos chama-las de , , e , de forma que um vetor solução seria da forma:
Para que um sistema com 4 equações e 4 incógnitas não tenha solução, o que deve acontecer é haver duas ou mais linhas que são incompatíveis.
Olha esse exemplo:
O sistema é impossível, porque não pode ser 1 e 4 ao mesmo tempo.
Agora vamos ver caso a caso e analisar em qual deles a solução pode não existir.
Passo 2

Repare que a terceira e a quarta linha têm os quadradinhos e zeros nas mesmas posições.
Nessas linhas, podemos ter uma relação que mostra inconsistência entre as equações e a solução pode não existir.
Podemos ter, nessas duas linhas, por exemplo:
Ou seja, multiplicamos o lado esquerdo da primeira linha por 2, mas fizemos algo diferente com o lado esquerdo (multiplicamos por 3), e não existem números que satisfaçam essas duas condições simultaneamente.
Como uma situação desse tipo pode acontecer na matriz dada nessa alternativa, ela é a nossa resposta.
Mas vamos continuar vendo as outras alternativas e ver por que a solução pode existir em cada uma delas.
Passo 3

Note que nesse caso, conseguimos tirar da segunda equação o valor de .
Substituindo na quarta equação, temos o valor de
Substituindo os dois na primeira, obtemos e, por fim, tiramos da última equação.
Então, esse sistema tem solução.
Passo 4

Seguindo a mesma ideia de antes, conseguimos achar na segunda equação.
Colocando na terceira, achamos .
Se substituirmos na quarta equação, achamos .
Por último, conseguimos encontrar a partir da primeira equação.
Então, o sistema tem solução.
Passo 5

Agora, obtemos na primeira equação.
Substituindo esse valor na última, obtemos .
Substituindo o valor de na terceira, obtemos .
A partir dos valores de e , usamos a segunda equação para encontrar .
Logo, o sistema tem solução.
O único caso em que a solução não necessariamente existe é no sistema da letra (a).
Resposta
