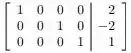P1 de Álgebra Linear da UFRJ - 2022.2

Um sistema em variáveis:

(A) com equações tem infinitas soluções.

(B) homogêneo com equações pode ter infinitas soluções.

(C) com equações tem solução única.

(D) com equações não tem solução.

Seja um polinômio de grau que passa pelos pontos. Então vale:

(A)

(B)

(C)

(D)

Q3: Seja A uma matriz tal que. Podemos afirmar que o se guinte vetor é uma solução de .

(A)

(B)

(C)

(D)

Assinale o conjunto solução de

(A)

(B)

(C)

(D)

Considere o sistema linear representado pela seguinte matriz aumentada:

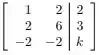
O valor de tal que o sistema tem solução é:

(A)

(B)

(C)

(D)

Q6: Qual dos hiperplanos abaixo não intercepta a reta

(A)

(B)

(C)

(D)

Considere as afirmativas abaixo:

I - Se um sistema admite solução então o conjunto de todas as colunas da matriz aumentada do sistema é linearmente independente.

II - Se o conjunto das colunas da matriz de coeficientes

de um sistema linear é linearmente independente, então o sistema tem solução única.

(A) Apenas I é verdadeira.

(B) Apenas II é verdadeira.

(C) Todas são falsas.

(D) Todas são verdadeiras.

(E) Não sei

pode ser descrito como o conjunto das triplas tais que:

(A)

(B)

(C)

(D)

Resolva o sistema linear abaixo

O valor de é:

(A)

(B)

(C)

(D)

Sabendo que o ponto pertence à reta , calcule o valor de .

(A)

(B)

(C)

(D)

Considere os planos definidos por tais

A interseção desses planos pode ser escrita como:

(A)

(B)

(C)

(D)

é o conjunto solução de qual das equações abaixo?

(A)

(B)

(C)

(D)

Assinale uma forma escalonada da matriz:

(A)

(B)

(C)

(D)

Sejam matrizes . Considere as afirmativas abaixo:

1- Se tem infinitas soluções, então tem infinitas soluções

2- Se tem solução, então podemos garantir que tem solução para todo .

(A) Apenas I é verdadeira.

(B) Todas são verdadeiras.

(C) Apenas II é verdadeira.

(D) Todas são falsas.