UFRJ; Sem campus; Álgebra Linear 2; P1; 2022.2; Questão 5
Considere o sistema linear representado pela seguinte matriz aumentada:
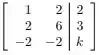
O valor de tal que o sistema tem solução é:
(A)
(B)
(C)
(D)
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Dessa vez um para resolver sistema linear .
Bem, queremos o valor de para que o sistema abaixo tenha solução
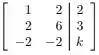
Para isso, vamos escalonar esse sistema
Passo 2
Vamos começar a escalonar a matriz aumentada
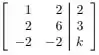
Para isso, fazemos , e obtemos
A partir daqui, já podemos encontrar uma solução para o sistema.
da segunda linha da matriz aumentada, temos que
Substituindo esse valor na primeira linha do sistema, temos que
Agora, se o sistema tem solução, então é tal que para e , a terceira linha do sistema é válida, ou seja, temos que
Logo
Valor presente na alternativa
Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊