Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Resolvendo Sistemas Lineares

Ver Teoria
Exercício 79123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778

Enunciado

UFRJ; Sem campus; Álgebra Linear 2; P1; 2022.2; Questão 4

Assinale o conjunto solução de

x 1 + x 2 + x 3 - x 4 = - 1

x 1 + 2 x 2 - x 3 = - 3

x 1 + 3 x 2 - 3 x 3 + x 4 = - 5

(A) ( 0 ,   - 1 ,   0 ,   0 ) +   s p a n { - 3 ,   2 ,   1 ,   0   } .

(B) ( 1 ,   - 2 ,   0 ,   0 ) +   s p a n { ( - 3 ,   2 ,   1 ,   0 ) , ( 2 ,   - 1 ,   0 ,   1 ) }   .

(C) ( 0 ,   - 1 ,   0 ,   0 ) +   s p a n { ( - 3 ,   2 ,   1 ,   0 ) , ( 2 ,   - 1 ,   0 ,   1 ) }  

(D) ( 1 ,   - 2 ,   0 ,   0 ) +   s p a n { ( 2 ,   - 1 ,   0 ,   1 ) }   .

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Dessa vez um para resolver sistema linear

x x 1 + x 2 + x 3 - x 4 = - 1

x 1 + 2 x 2 - x 3 = - 3

x 1 + 3 x 2 - 3 x 3 + x 4 = - 5

Então vamos à luta!

Passo 2

Queremos resolver

x x 1 + x 2 + x 3 - x 4 = - 1

x 1 + 2 x 2 - x 3 = - 3

x 1 + 3 x 2 - 3 x 3 + x 4 = - 5

Escrevendo esse sistema na forma de matriz aumentada temos:

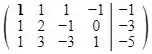
Vamos fazer L 2 ← L 2 - L 1

Por fim, fazemos L 3 ← L 3 - L 1 - 2 L

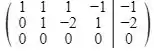
Ou seja, nosso sistema só tem duas equações relevantes. Logo como temos duas equações e quatro variáveis o sistema terá infinitas soluções. Mas como elas serão?

Passo 3

Chegamos no seguinte sistema escalonado:

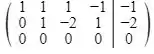
Fazendo x 3 e x 4 como variáveis livres, isto é, dizemos que x 3 = s e x 4 = t , com s , t   ∈ R . A solução do nosso sistema fica:

x 2 = 2 s - t - 2

e substituindo na primeira equação do sistema escalonado, temos:

x 1 = - 2 s + t + 2   - s + t - 1

= - 3 s + 2 t + 1

Logo, a solução desse sistema é:

( - 3 s + 2 t + 1,2 s - t + 2 , s , t )

que pode ser expressa como:

( 1 , - 2,0 , 0 ) + s ( - 3,2 , 1,0 ) + t ( 2 , - 1,0 , 1 ) ,   c o m   s , t   ∈ R

Ou seja, a nossa solução é qualquer vetor em

( 1 ,   - 2 ,   0 ,   0 ) +   s p a n { ( - 3 ,   2 ,   1 ,   0 ) , ( 2 ,   - 1 ,   0 ,   1 ) }  

Esse vetor se encontra na alternativa b )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

b )

Exercícios de Livros Relacionados

Para cada sistema do Exercício 3 que for linear, determine se é consistente.
Em cada parte, determine se as equações formam um sistema linear no sistema: - 2 x + 4 y + z = 2 3 x - 2 y = 0
Na linha do exercício anterior, mostre que se a1b2 − a2b1 ≠ 0 então o sistema admite sempre uma solução do tipo (x, y, 0).
No sistema abaixo, atribua sucessivamente valores aos parâmetros m, n de modo que as três equações representem um único plano, dois planos ou três planos: x-2 y-3 z=m3 x-6 y-9 z=n- 2 x+4 y+6 z=1
Para cada um dos sistemas abaixo, decida em qual dos casos (primeiro a oitavo) discutidos no texto ele se enquadra. Determine também todas as soluções do sistema, se houver. 3 x-5 y+2 z=14 x-3 y+z=22