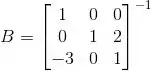P2 de Álgebra Linear da UFRJ - 2018.2

A soma das entradas de B é:

(a) -6

(b) -2

(c) 4

(d) 8

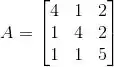
A dimensão do autoespaço de A associado ao autovalor 3 é:

(a) 0

(b) 1

(c) 2

(d) 3

Seja

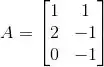
a matriz da transformação linear (em relação à base canônica). Se o vetor x tem coordenadas (1,1) em relação à base , então vale:

(a) (3,3,-1)

(b) (3,3,-2)

(c) (2,1,-1)

(d) (2,1,1)

Sejam A e B duas matrizes. Considere as afirmações.

(I) Se o produto AB está definido, então o produto BA também está.

(II) Se os produtos AB e BA estão definidos, então A e B são quadradas.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é falsa e (II) é verdadeira.

Sejam A e B matrizes tais que o produto AB está definido. Considere as afirmações:

(I) Se , então é subespaço de .

(II) contém .

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Se (1,1) e (2,1) são autovetores de A associados aos autovalores 2 e -1, respectivamente, calcule .

(a)

(b)

(c)

(d)

Os autovalores da matriz

são:

(a) -1 e 3

(b) -1 e 4

(c) -2 e 2

(d) -2 e 3

Seja A uma matriz . Considere as afirmações:

(I) Se então A é necessariamente injetiva.

(II) Se A é injetiva, então .

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Seja . Considere as afirmações.

(I) Existe um vetor não nulo tal que suas coordenadas na base canônica são o quádruplo de suas coordenadas na base .

(II) Existe um vetor não nulo tal que suas coordenadas na base canônica são o triplo de suas coordenadas na base .

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é falsa e (II) é verdadeira.

Qual matriz abaixo é diagonalizável (sobre os reais)?

(a)

(b)

(c)

(d)

A matriz

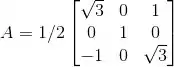
é uma rotação de radianos em torno do eixo y em Assinale abaixo a matriz .

Dica: não é uma boa ideia fazer a conta “na força bruta”,

A matriz que tem autovetores e associados, respectivamente, aos autovalores 2 e 3 é:

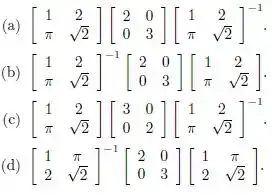
Seja A uma matriz . Considere as afirmações:

(I) Necessariamente,

(II) pode ser 3.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Seja T uma transformação linear tal que e . A matriz associada a T é:

(a)

(b)

(c)

(d)

Seja C uma matriz tal que o sistema tem solução única. Considere as afirmações.

(I) É possível que C seja um produto de matrizes C = AB onde A é e B é

(II) É possível que C seja um produto de matrizes C = AB onde A é e B é

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Seja A a matriz que representa, em relação à base canônica, a projeção ortogonal sobre a reta de equação . A soma das entradas de A é:

(a) 15/13

(b) 20/13

(c) 25/13

(d) 30/13