Seja
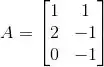
a matriz da transformação linear (em relação à base canônica). Se o vetor x tem coordenadas (1,1) em relação à base , então vale:
(a) (3,3,-1)
(b) (3,3,-2)
(c) (2,1,-1)
(d) (2,1,1)
Passo 1
O enunciado disse que a matriz A é a matriz da transformação T escrita na base canônica.
Isso significa que, pra fazermos T(x) usando a matriz A, o vetor x tem que estar na base canônica!!!
Então tomem cuidado, porque o vetor x que foi dado está escrito na base que não é a base canônica do .
Passo 2
Antes de fazermos o produto Ax, vamos ter que escrever o vetor x na base canônica.
E como eu faço isso??
Se eu tenho as coordenadas do vetor em uma base, é só eu fazer a combinação linear dos vetores da base em ordem!!
Então, se x tem coordenadas (1,1) na base , pra achar x na base canônica vamos fazer:
Agora sim eu posso fazer o produto Ax e achar T(x)!
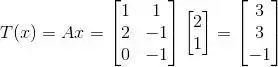
Resposta
(a) (3,3,-1)