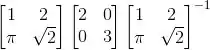A matriz que tem autovetores e associados, respectivamente, aos autovalores 2 e 3 é:
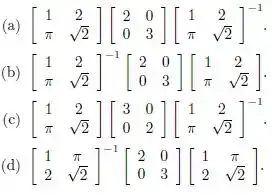
Passo 1
Olhando pras alternativas, percebemos que a questão quer que a gente escreva a matriz como:
Onde P é a matriz dos autovetores nas colunas e D a matriz diagonal com autovalores na diagonal principal.
Então a matriz P vai ser:
Como o autovetor aparece primeiro, o primeiro autovalor que vai aparecer na diagonal da matriz D vai ser o autovalor associado a , que é o 2.
Então a matriz D fica:
Temos também:
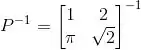
Então:
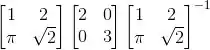
Resposta
(a) 
Exercícios de Livros Relacionados
Seja A =4 0 1 2 3 2 1 0 4 Será A diagonalizável? Justifique sua conclusão.
Dizemos que uma matriz A n × n é diagonalizável se seu operador associado T A : R n → R n for diagonalizável, ou seja, A é diagonalizável se, e somente se A admitir n autovetores L I . Baseado nisto,
Dizemos que uma matriz A n × n é diagonalizável se seu operador associado T A : R n → R n for diagonalizável, ou seja, A é diagonalizável se, e somente se A admitir n autovetores L I . Baseado nisto,
Dizemos que uma matriz A n × n é diagonalizável se seu operador associado T A : R n → R n for diagonalizável, ou seja, A é diagonalizável se, e somente se A admitir n autovetores L I . Baseado nisto,
Dada a matriz: A = 2 1 0 0 0 2 0 0 0 0 2 0 0 0 0 3 A é diagonalizável?Encontre seu polinômio minimal.