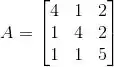
A dimensão do autoespaço de A associado ao autovalor 3 é:
(a) 0
(b) 1
(c) 2
(d) 3
Passo 1
Para achar o autoespaço associados a um autovalor , precisamos fazer:
Como foi dado :
Fazendo essa conta com a matriz A dada e escrevendo na forma de uma matriz aumentada:

Se , temos uma equação:
Isolando uma das variáveis, por exemplo o x:
Então os vetores v vão ser:
Como e são LI (um não é múltiplo do outro), então esses 2 vetores formam uma base para o autoespaço associado a
Como há 2 vetores nessa base, a dimensão desse autoespaço é 2.
Resposta
(c) 2