P3 de Álgebra Linear da UFRJ - 2016.1

Calcule a soma dos módulos dos autovalores da matriz

Qual dos vetores abaixo é ortogonal ao vetor e pertence ao plano gerado pelos vetores e ?

Assinale, dentre os sistemas abaixo, aquele cujo conjunto-solução é o plano gerado pelos vetores e :

Seja uma transformação linear cuja imagem é o plano e o núcleo é a reta que passa pela origem na direção do vetor . Assinale a matriz que pode representar :

Seja um subespaço vetorial de tal que :

1. Existe uma matriz , tal que
2. Existe uma matriz , tal que

Ambas são falsas.

Ambas são verdadeiras.

A é verdadeira e é falsa.

é falsa e é verdadeira.

Sejam e vetores do tal que e . Pode-se afirmar que, necessariamente,

1. e são ortogonais

é verdadeira e é falsa

Ambas são verdadeiras

Ambas são falsas

é falsa e é verdadeira

Seja o espaço gerado pelas linhas de . Qual a dimensão do complemento ortogonal de ?

Seja o vetor do plano que é o mais próximo do vetor . Então a soma de suas entradas , vale:

Seja um conjunto ortonormal de vetores não nulos:

é verdadeira e é falsa

Ambas são verdadeiras

Ambas são falsas

é falsa e é verdadeira

Seja uma matriz . Assinale a alternativa correta:

A equação que modela um determinado fenômeno físico é dada pela função . Alguns experimentos foram realizados com os seguintes resultados:

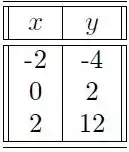
Os valores de , de forma a obter a melhor aproximação no sentido dos mínimos quadrados são:

,

,

,

Considere as seguintes afirmações:

1. Se é um conjunto ortonormal que gera o subespaço , então é uma base ortogonal de .
2. O sistema linear sempre tem solução mesmo quando

Qual das opções abaixo é CORRETA?

A afirmativa é verdadeira e é verdadeira

A afirmativa é verdadeira e é falsa

A afirmativa é falsa e é verdadeira

A afirmativa é falsa e é falsa

Considere as seguintes afirmações:

1. O núcleo e o espaço linha de uma matriz real são subespaços do e a soma de suas dimensões é igual a .
2. O espaço linha e o espaço coluna de qualquer matriz real são subespaços, respectivamente, do e do , e suas dimensões são iguais.

Qual das opções abaixo é CORRETA?

A afirmativa é verdadeira e é falsa

A afirmativa é verdadeira e é verdadeira

A afirmativa é falsa e é verdadeira

A afirmativa é falsa e é falsa

Considere as seguintes afirmações:

1. Existe uma transformação linear que é sobrejetiva.
2. Existe uma transformação linear tal que a dimensão do núcleo seja igual à da imagem.

Qual das opções abaixo é a CORRETA?

A afirmativa é falsa e é falsa

A afirmativa é falsa e é verdadeira

A afirmativa é verdadeira e é falsa

A afirmativa é verdadeira e é verdadeira

Assinale abaixo a área do paralelogramo definido pelos vetores e em :

Seja uma transformação linear que multiplica o vetor por e o vetor por . Seja a matriz de . Calcule a soma dos elementos da diagonal principal de .