A3 T4
Seja um conjunto ortonormal de vetores não nulos:
é verdadeira e é falsa
Ambas são verdadeiras
Ambas são falsas
é falsa e é verdadeira
Passo 1
Então esse é o tipo de questão que saí na intuição! Tentar provar isso dá um trabalhinho chato e ninguém quer perder tempo de prova né! Se liga, pensa em três vetores ortonormais no ! Pode ser os vetores diretores , e mesmo! Você tem algo assim:
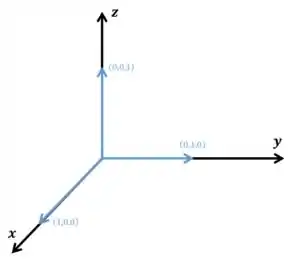
Agora que vem a tal da intuição. Concorda que se você somar ou subtrair quaisquer vetores desses entre si, vai dar um vetor com mesmo módulo mas com a direção diferente? A soma seria assim:
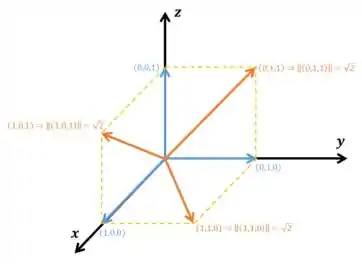
E a diferença assim:
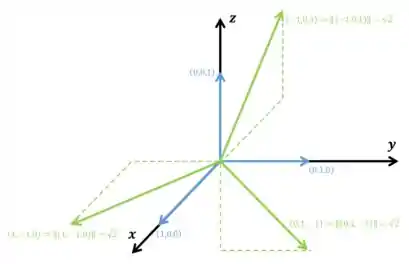
Visualizou? E isso vale pra quaisquer vetores ortonormais! Daria a mesma coisa só que rodado! Então ambas são verdadeiras.
Resposta
Letra
Exercícios de Livros Relacionados
Considere R 2 ,R 3 e R 4 com o produto interno euclidiano. Em cada parte, encontre o cosseno do ângulo entre u e v . u = 1 , - 3 , v = 2,4 u = - 1,0 , v = 3,8 u = - 1,5 , 2 , v = 2,4 , - 9 u = 4,1 , 8
13. Quais as condições devem satisfazer a e b para que a matriz a + b b - a a - b b + a seja ortogonal?
Dizemos que um operador matricial R 2 é rígido se mantiver o comprimento dos vetores, e preserva ângulo se não mudar o ângulo entre vetores não nulos.(a) Dê o nome de dois tipos distindos de operadore
O resultado do Exercício 15 tem um análogo para matrizes ortogonais 3 × 3 , como segue. Pode ser provado que a multiplicação ortogonal A de tamanho 3 × 3 é uma rotação em torno de algum eixo se d e t
7. Repita o Exercício 6 com theta = (pi)/(3) .