P1 de Cálculo 1 da UFRJ - 2016.2

Calcule o limite:

Suponha que e sejam, ambas, funções diferenciáveis satisfazendo para todo . Então podemos afirmar que os gráficos de e :

1. Não possuem mais do que uma interseção.
2. Possuem exatamente uma interseção.
3. Podem possuir mais de uma interseção.
4. Não possuem interseção.
5. Têm uma reta tangente em comum no ponto de interseção.

Seja derivável e suponha que o gráfico da derivada seja dado por:

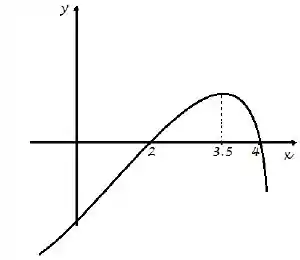
Considere as seguintes afirmações:

1. A função tem um mínimo local em e um máximo local em .
2. O gráfico de côncavo para baixo em .
3. A função tem um ponto de inflexão em .

Então:

1. Apenas as afirmações (I) e (III) estão corretas.
2. Apenas as afirmações (II) e (III) estão corretas.
3. Apenas as afirmações (I) e (II) estão corretas.
4. Todas as afirmações estão corretas.
5. Apenas a afirmação (I) está correta.

Calcule o limite:

Sejam e números reais tais que:

Mostre que o polinômio possui ao menos uma raíz no intervalo .

Dica: Use o polinômio:

Considere a função com derivadas e dadas por:

1. Dê o domínio de definição de .
2. Determine as assíntotas horizontais e verticais, caso existam.
3. Identifique os pontos críticos, os extremos relativos e os intervalos onde a função é crescente e onde é decrescente.
4. Encontre os pontos de inflexão de , se houver, e os intervalos de concavidade para cima e para baixo.
5. Usando as informações anteriores, faça um esboço do gráfico de .

Sejam , : funções diferenciáveis tais que:

Então a derivada da função no ponto é:

1. .
2. .
3. .
4. .
5. .

A reta é paralela à reta tangente à elipse no ponto com coordenadas:

1. , .
2. , .
3. , .
4. , .
5. , .

Sobre a equação , é correto afirmar:

1. Admite solução no intervalo .
2. Não admite solução real.
3. Admite solução no intervalo .
4. Admite solução no intervalo
5. Admite solução no intervalo .

Suponha que:

Para todo . Sobre o limite é correto afirmar que:

1. Seu valor é .
2. Seu valor é .
3. Seu valor depende de qual é a função .
4. Seu valor é .
5. Seu valor é .

Suponha que para todo . Considere as seguintes afirmações:

1. é contínua em .
2. é diferenciável em .
3. .

É verdadeira ou são verdadeiras:

1. Todas as três afirmativas.
2. Somente a afirmativa (II).
3. Somente a afirmativa (I).
4. Nenhuma das afirmativas.
5. As afirmativas (I) e (II).

Considere uma função satisfazendo:

Então, vale necessariamente que:

1. .
2. não existe.
3. não está definida em .
4. .

Calcule a derivada da função:

Determine a equação da reta tangente à curva no ponto em que .

Determine o valor de para que a função seja contínua, com:

Seja uma função duas vezes diferenciável. Considere:

Então , onde

1. .
2. .
3. .
4. .
5. .

Considere a reta tangente ao gráfico de em . Se está nessa reta, então: