Seja derivável e suponha que o gráfico da derivada seja dado por:
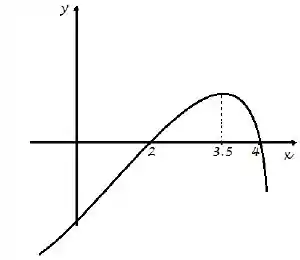
Considere as seguintes afirmações:
- A função tem um mínimo local em e um máximo local em .
- O gráfico de côncavo para baixo em .
- A função tem um ponto de inflexão em .
Então:
- Apenas as afirmações (I) e (III) estão corretas.
- Apenas as afirmações (II) e (III) estão corretas.
- Apenas as afirmações (I) e (II) estão corretas.
- Todas as afirmações estão corretas.
- Apenas a afirmação (I) está correta.
Passo 1
A primeira coisa a notar aqui é que o gráfico é da derivada da função e a pergunta é sobre a função! Então temos que ter bastante cuidado com isso.
O gráfico da derivada, porém, já nos dá bastante informação, é só lembrar que a derivada é a taxa de variação da função.
Então vamos lá, analisando cada uma das afirmações. Pela afirmação (I) a função tem um mínimo em . Para que isso seja verdade, precisamos que seja um ponto critico e que a derivada seja negativa à esquerda e positiva à direita deste ponto.
Observando o gráfico, percebemos que é de fato um ponto crítico, pois a derivada vale zero nesse ponto e também é ponto de mínimo, pois a derivada é negativa à esquerda e positiva à direita.
Outra parte da afirmação é que é um ponto de máximo. Ele já é um ponto crítico, pois a derivada é zero nesse ponto, também será um ponto de máximo pois a derivada é positiva à esquerda e negativa à direita.
Logo, concluímos que a afirmação (I) é verdadeira!
Passo 2
Vamos para afirmação (II). Para que seja verdade, precisamos que o gráfico de seja côncavo para baixo em . Para que seja côncavo para baixo, precisamos que a segunda derivada seja negativa.
Ué, mas o gráfico aí é da primeira derivada!! Calma, jovem. Só lembrar que a segunda derivada é a taxa de variação da primeira. Repara alí que em , a derivada está crescendo, logo sua variação é positiva é . Dessa maneira, será côncava para cima e a afirmação (II) é falsa!
Passo 3
Vamos para última agora, Para que (III) seja verdadeira, precisamos que a função tenha um ponto de inflexão em . O ponto de inflexão ocorre onde a função muda de concavidade.
Veja que a derivada está crescendo à esquerda desse ponto, logo será côncava para cima e está decrescendo para valores à direita de , logo será será côncava para baixo aí. Dessa maneira, houve uma troca de concavidade e é um ponto de inflexão bem simpático.
Assim, concluímos que a afirmação (III) é verdadeira e a resposta correta é a alternativa (a)!
Resposta
Alternativa (a).