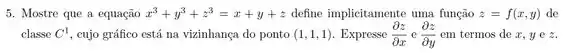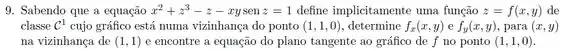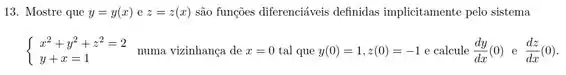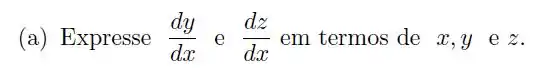Listas GMA de Cálculo IIB da UFF - Lista 12

Considere

É possível, pelo Teorema da Função Implícita, garantir que esta equação define implicitamente uma única função , com numa vizinhança de e numa vizinhança de , quando ?

Considere

É possível, pelo Teorema da Função Implícita, garantir que esta equação define implicitamente uma única função , com numa vizinhança de e numa vizinhança de , quando ?

Seja definida por

1. Faça um esboço das curvas de nível de associadas aos níveis , e .
2. Faça um esboço do gráfico de .
3. Mostre que pertence a curva de nível

De associada ao nível .

4. Mostre que e
5. Mostre que a curva de nível pode ser representada como o gráfico de uma função com .
6. Este exercício constitui um contraexemplo para o teorema da função implícita para ? Justifique cuidadosamente sua resposta.

11. A função de classe , é dada pela equação ( é um real fixo), onde é da classe e . Verifique que

12. Sabendo-se que a função define implicitamente uma função de classe cujo gráfico está na vizinhança do ponto determine a taxa de variação de no ponto , na direção e sentido do vetor .

Suponha que e estão definidas implicitamente pelo sistema

Encontre todas as derivadas parciais de e em termos de ,, , e .

Se e são dadas implicitamente pelo sistema:

Mostre que:

As equações

Definem , e como funções de e próximo ao ponto , , ? Calcule as derivadas parciais e em

Seja , onde e são dadas implicitamente por

a)Mostre que

b)Suponha que . Calcule .

Considere

É possível, pelo Teorema da Função Implícita, garantir que esta equação define implicitamente uma única função , com numa vizinhança de e numa vizinhança de , quando ?

Dado do sistema

1. Verifique que o sistema define implicitamente na vizinhança de e tal que
2. Determine
3. Determine a função afim que aproxima na vizinhança de
4. Calcule, aproximadamente,